Saignées sous les tropiques
Le médecin allemand Julius von Mayer a été le premier à énoncer, dès 1841, le principe de conservation de l’énergie. Ce principe stipule que l’énergie totale d’un système se conserve, quoi qu’il arrive. Car, dès 1840 Mayer s’embarque sur un vaisseau hollandais à destination de Java. Arrivé à destination, il pratique des saignées sur des matelots malades. Lors de la première saignée, il constate que le sang de la veine est d’un rouge extrêmement brillant. Il pense donc d’abord avoir touché une artère. En effet, le sang veineux se charge des déchets du métabolisme. Il transporte donc moins d’oxygène que le sang artériel et apparaît de ce fait généralement plus foncé.
Toutefois, il constate que le phénomène se reproduit sur tous les marins subissant une saignée. Il en déduit donc qu’à Djakarta le sang veineux est systématiquement plus rouge qu’en Allemagne. Il explique ce phénomène par le fait que, sous les tropiques, le corps utilise moins d’oxygène pour maintenir sa température à 37°C. Car, là-bas il fait chaud alors qu’en Europe, il fait plus froid. Or, d’après la théorie de Lavoisier, c’est la combustion des aliments qui fournit l’énergie pour faire fonctionner le corps humain. Il apparaît donc possible de transformer l’énergie des aliments soit en travail musculaire, soit en chaleur corporelle.
Pâte à papier et dynamos
Ainsi, dans un corps humain, l’oxydation d’une certaine quantité de nourriture s’accompagne toujours de la production d’une certaine quantité de chaleur. Par conséquent, il est impossible de créer de l’énergie. On ne peut que seulement la transformer d’une forme particulière dans une autre forme particulière. De retour en Allemagne, Mayer soumet dès 1841 un papier lourd et maladroit à un journal de physique allemand. Ce papier est ignoré par l’éditeur, car Mayer est médecin et n’y connaît rien en physique et en mathématiques.
En 1842, il augmente donc ses connaissances en physique. Il publie alors un papier où il mesure la hausse de température dans de la pâte à papier remuée avec l’aide d’un cheval. Il calcule que cette hausse est telle qu’une grande calorie de chaleur équivaut à 365 kgf·m de travail mécanique (soit environ 3,65 kJ·kcal-1). La même année, il montre que la chaleur spécifique d’un gaz à pression constante Cp est supérieure à la chaleur spécifique mesurée à volume constant CV.
Mayer reste fidèle à son hypothèse d’équivalence entre énergie mécanique et chaleur. Il suggère donc que cette différence de chaleur ΔQ = (Cp – CV)·Δθ, soit due au travail d’expansion mécanique du gaz contre la pression atmosphérique lors de la mesure de Cp. En 1843, il mesure le travail mécanique fourni par une dynamo plongée dans un bain d’eau. Grâce à l’élévation de température du bain , il trouve une nouvelle valeur de l’équivalent chaleur-travail de 460 kgf·m (soit environ 4,60 kJ·kcal-1).
Effet Joule
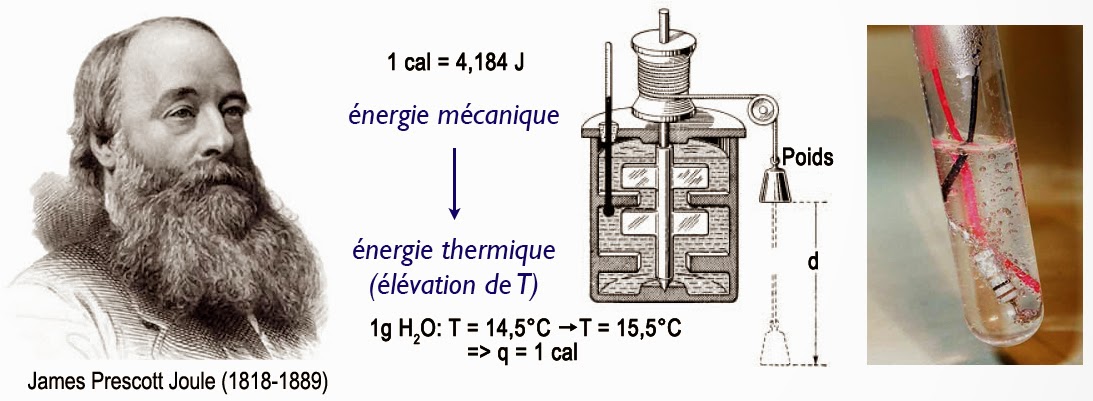
Pendant que Mayer méditait sur la couleur du sang des marins voyageant sous les tropiques, le fils d’un brasseur de bière anglais James Prescott Joule se posait lui aussi des questions. Joule était fasciné par les phénomènes électriques et avait installé un laboratoire privé dans la maison familiale. En 1840, il mesura que la quantité de chaleur ΔQ produite chaque seconde dans une résistance traversée par un courant électrique. Il constata alors que cette chaleur était proportionnelle à la résistance électrique R du matériau et au carré de l’intensité I du courant électrique : ΔQ = R·I2·Δt.
Ce phénomène s’appelle de nos jours l’effet Joule. Il montrait qu’il était possible de transformer l’énergie électrique en chaleur. Or, Joule était pétri d’idées religieuses concernant l’unité des forces dans la nature. Il entreprit donc dès 1841 de mesurer de manière extrêmement précise un hypothétique équivalent universel. Le but était de pouvoir convertir l’unité de chaleur, la calorie, en une unité de travail mécanique, le kgf·m.
Force vive et énergie cinétique
Sur le plan théorique, Joule rejeta la théorie alors acceptée du calorique défendue par Antoine Lavoisier et Sadi Carnot. Cette théorie soutenait que le calorique ne pouvait être ni créé ni détruit. Joule démontrait au contraire par ses expériences très précises que chaleur et travail étaient deux formes équivalentes d’une nouvelle quantité physique. Il identifia cette dernière à la vis viva (force vive) définie en 1693 par le scientifique allemand Gottfried Wilhelm Leibniz. Ce dernier définissait cette force vive comme étant le produit de la masse par le carré de la vitesse. Cette force vive s’appelle aujourd’hui “énergie cinétique”.
En effet, Leibniz avait remarqué que selon les lois de la mécanique Newtonienne, il était également possible de transformer l’énergie cinétique en énergie potentielle. De plus, la somme de ces deux énergies semblait être une constante du mouvement. Le problème était que cette loi de conservation de l’énergie mécanique n’était plus valide dès qu’il y avait des frottements. Mayer et Joule vont donc par deux approches très différentes faire le rapprochement entre toutes ces formes d’énergie : cinétique, potentielle, chimique, mécanique et chaleur.
Conservation de l’énergie totale
L’hypothèse commune à Mayer et Joule était que l’énergie totale était une quantité toujours conservée. Alors que ceci n’était pas le cas pour chacune des formes d’énergie prises individuellement. En effet, on disposait d’une part d’une loi de conservation de l’énergie mécanique qui était violée dès qu’il y avait frottement. Il y avait, d’autre part, la loi de conservation du calorique qui était violée dès qu’il y avait production de travail mécanique. Mayer et Joule proposèrent donc de parler tout simplement d’énergie totale (mécanique + chaleur). Les deux problèmes se trouvaient ainsi résolus d’un coup. En 1841, ils énoncent, chacun de leur côté, le principe de conservation de l’énergie totale sous la forme : « l’énergie ne peut être ni être créée, ni être détruite ».
Toutefois, cette belle idée ne va pas être tout de suite acceptée par la communauté scientifique. En effet, le prestige de Lavoisier est alors immense. Mayer n’est un simple médecin avec des connaissances en physique très rudimentaires. De même, Joule n’est qu’un simple brasseur de bière qui s’amuse dans sa cuisine avec des résistances électriques et des aimants. Pourtant, dès 1847, Joule avait une valeur de l’équivalent travail-chaleur précise à 99%. Car, il était capable selon ses dires de mesurer la température avec une précision de 1/200 de degré Fahrenheit. Or, bien de peu de physiciens chevronnés de l’époque étaient capables d’une telle prouesse.
Joule ou Mayer ?
En fait, ce que les physiciens académiques ignoraient, c’est que pour réussir une bonne bière, il fallait un contrôle de la température extrêmement précis. Et, que les meilleurs thermomètres se trouvaient donc pour des raisons financières de profit chez les brasseurs et non dans les laboratoires… À l’opposé, les valeurs proposées par Mayer étaient toutes discordantes. Car, ce dernier ne disposait que de très peu de moyens. Par conséquent, ses idées étaient plus basées sur la théorie que sur l’expérience. Mais, en 1850, on commença à réaliser que la théorie du calorique de Lavoisier présentait de graves défauts. Or, l’on disposait pour la remplacer de la théorie de la conservation de la force vive. Celle-ci était basée sur les idées originales de Mayer et sur les mesures extrêmement précises de Joule.
La communauté scientifique ignora donc les mesures peu nombreuses et disparates de Mayer. En revanche, elle couvrit Joule de lauriers en lui attribuant la paternité de la découverte du principe de conservation de l’énergie. Face à cette situation, Mayer fut terriblement déçu et frustré au point qu’il tenta de se suicider. Son acte manqué lui valu la fréquentation pendant de longues années d’asiles psychiatriques.
Forces vives, mortes et vitales
Il faudra attendre 1863 pour que le physicien anglais John Tyndall réhabilite le travail de pionnier de Mayer. Il lui attribua donc la paternité du principe de conservation de l’énergie. Car, Joule n’avait aucune expérience en biologie. Seul Mayer avait compris dès 1845 que lors de la synthèse chlorophyllienne, il y avait conversion de l’énergie lumineuse en énergie chimique. Seul Mayer avait donc saisi toute la portée de ce principe de conservation de la force vive. Car, il s’appliquait dans tous les domaines de la science : physique, chimie et biologie. Pour sa part, Joule, brillant expérimentateur, s’était borné au seul domaine de la physique.
On notera qu’au cours de cette première moitié du XIXᵉ siècle, le terme force vive de Leibniz était systématiquement préféré au terme énergie. Ce dernier terme avait été introduit dès 1807 par le physicien anglais Thomas Young. Il dérive du grec έν-ἔργον signifiant littéralement « en travail » ou « être actif ». À l’opposé de cette force vive, il y avait la force morte. Celle-ci se mesurait en kgf et non en kgf·m comme la force vive. D’un autre côté on commençait à se rendre compte grâce aux travaux de Mayer que les forces vitales qui animaient la matière biologique ne différaient en rien des forces naturelles rencontrées en physique et en chimie.
Physiologie
Le physiologiste allemand Hermann von Helmholtz ne croyait pas non plus aux forces vitales biologiques. Il était l’inventeur du premier ophtalmoscope. Il fut aussi le premier à mesurer la vitesse de propagation de l’influx nerveux (v = 26 m·s-1) dans un nerf sciatique de grenouille. En 1847, il publia un mémoire où il montra que la force de tension produit de la force par la distance peut être transformée en force vive, produit de la masse par le carré de la vitesse. Lui aussi, énonça de manière indépendante de Mayer ou Joule, le principe de conservation de l’énergie.
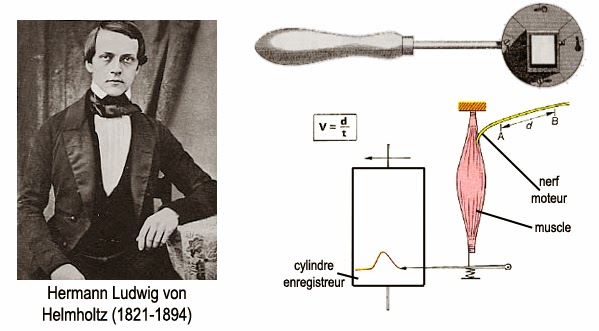
On notera toutefois que contrairement à Mayer ou Joule, Helmholtz se contenta d’une démonstration purement mathématique de cette équivalence. Il appela son principe “principe de conservation de la force vive” :
\frac{1}{2}m\cdot{\rm{v}}_B^2 - \frac{1}{2}m\cdot{\rm{v}}_A^2 = - \int_A^B {f\cdot dr}Ici, f est la force qui agit sur la masse m qui se déplace du point A au point B avec une vitesse v. Pour Helmholtz, le produit f·dr qu’il appelle force de tension est une grandeur qui a la dimension d’un travail. Cette force est consommée par le mouvement acquis. C’est-à-dire que la variation de la force de tension se retrouve sous la forme d’une variation de la force vive.
Thermodynamique
Le terme énergie ne s’imposa en physique que vers 1850 via les travaux du physicien anglais William Thompson, futur Lord Kelvin. Ce fut Kelvin qui introduisit l’expression énergie cinétique au lieu du terme force vive. Pour sa part, le physicien écossais William Rankine remplaça l’expression force de tension par le terme énergie potentielle. À partir de 1850 le principe de conservation des forces vives de Mayer-Joule-Helmholtz devint donc le principe de conservation de l’énergie. Avec ce vocabulaire moderne, le premier principe de la thermodynamique peut être formulé de la manière suivante :
« Il existe une fonction d’état U représentant l’énergie totale du système. Cette fonction est telle que dans tout processus où l’on passe d’un état d’équilibre à un autre, la variation nette de cette énergie interne U est donnée par la différence entre la chaleur Q apportée au système et le travail W fourni par ce système ».
Pour des changements infinitésimaux, on peut donc écrire ce principe sous la forme différentielle dU = δQ – δW. Or, l’énergie interne d’un gaz parfait ne dépend que son volume V et de sa température θ. Pour une pression P, on peut donc écrire que δW = P·dV. Mathématiquement parlant, si l’on considère U comme une fonction de deux variables U(V,θ), le fait que U soit une fonction d’état signifie que la différentielle dU est une différentielle totale exacte. C’est-à-dire que l’intégrale entre deux états thermiques est indépendant du chemin d’évolution entre ces deux états :
\int_1^2 {dU} = U({V_2},{\theta _2}) - U({V_1},{\theta _1}) \Leftrightarrow \oint {\delta Q} = \oint {P\cdot dV}De manière équivalente, l’intégrale sur un chemin qui revient à l’état de départ doit être nulle. Ceci signifie que la chaleur totale absorbée par le système doit être égale au travail total effectué.
Unités d’énergie
Ces deux expressions mathématiques du premier principe de la thermodynamique sont équivalentes et apparemment triviales. Il est cependant important de bien comprendre le sens physique de ces notations. Tout d’abord, le fait qu’il soit possible de mesurer chaleur et travail avec la même unité, autorise de les additionner. Ceci implique d’abandonner soit la calorie, soit le kgf·m. La théorie du calorique ayant très mauvaise presse après 1850, on laissa tomber la calorie comme une vieille chaussette. On conserva donc le kgf·m.
Toutefois, comme chaleur et travail ne sont que deux formes différentes de l’énergie, on introduisit une nouvelle unité l’erg pour mesurer l’énergie quelle que soit sa forme. Vers la fin du XIXᵉ siècle, la nécessité se fit sentir de rationaliser le système d’unités électromagnétique. Car, entre-temps, il y avait eu unification des phénomènes électriques, magnétiques et optiques. On abandonna alors l’erg pour le newton·mètre (N·m). Cette dernière unité prit le nom de Joule (symbole J) en l’honneur de ce grand expérimentateur.
Dans ces conditions, on a les relations quantitatives suivantes : 1 cal = 4,184 J; 1 kgf·m = 9,8066 J et 1 erg = 10-7J. De nos jours, le joule est la seule unité autorisée lorsqu’on parle d’une certaine quantité d’énergie. Mis à part les diététiciens et quelques chimistes théoriciens qui s’acharnent encore à parler en calories, la consigne est assez bien respectée.
États d’équilibre et réversibilité
Il est aussi bon de rappeler que le premier principe ne concerne que des états d’équilibre. Car, hors équilibre, la notion de température devient dénuée de sens. Il doit donc être clair que le chemin d’intégration dans un plan (V, θ) doit être une succession d’états d’équilibre. En effet, les points appartenant à ce plan ne peuvent correspondre à des états de non-équilibre. Ceci pose la question de savoir comment suivre de tels chemins sur un plan expérimental. En effet, tout changement d’état implique de fait une perte d’équilibre.
Une solution est de considérer que la transformation doit se produire de manière infiniment lente. Ceci afin que chaque point du chemin suivi soit assimilable à un état d’équilibre. Cela signifie que le chemin d’intégration dans le plan (V, θ) correspond à la limite d’une suite d’états, où les changements entre les différents états ont lieu de manière infiniment lente.
Processus réversibles
Or, un tel processus où l’on reste à tout moment très proche de l’équilibre possède une autre propriété importante. Car, si la quantité de chaleur varie de manière infinitésimale, la variation de température qui en découle sera également infinitésimale. Ceci signifie forcément qu’un changement infinitésimal opposé de température sera capable de renverser le sens du flux de chaleur.
De même, si le volume varie d’une quantité infinitésimale, la différence de pression qu’elle provoque sera, elle aussi, infinitésimale. De ce fait, une variation infinitésimale opposée de pression sera capable de renverser la direction du mouvement. Autrement dit, un processus infiniment lent est de nature essentiellement réversible. Car, lorsqu’un système est arbitrairement proche de l’équilibre, alors une variation arbitrairement petite de son environnement peut renverser la direction du processus. Il s’ensuit que les différents chemins d’intégration qui interviennent dans la formulation mathématique du premier principe s’interprètent comme étant de nature réversible.
Dans la pratique, certains systèmes matériels tels que les gaz arrivent très rapidement à l’équilibre. Dans ces conditions, même des changements très rapides d’états à notre échelle de perception macroscopique représentent d’excellentes approximations de changements réversibles. Par exemple, pour des ingénieurs thermiciens, il est raisonnable d’admettre que les changements d’état de la vapeur d’eau dans les machines à vapeur sont de nature réversibles. Pour des liquides et surtout pour des solides, la notion de réversibilité s’applique aussi, mais ici le facteur temps devient crucial.



Leave a Reply