Rotation de la molécule d’eau

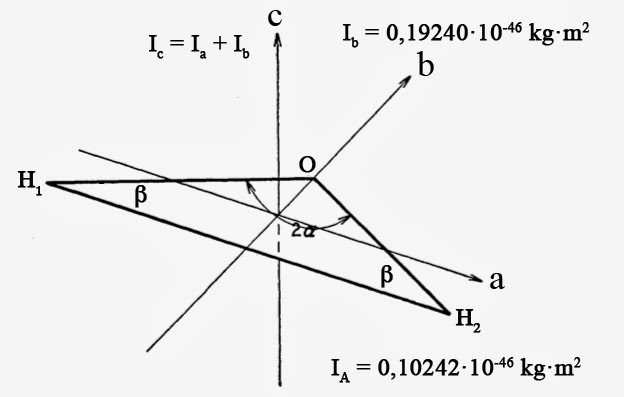
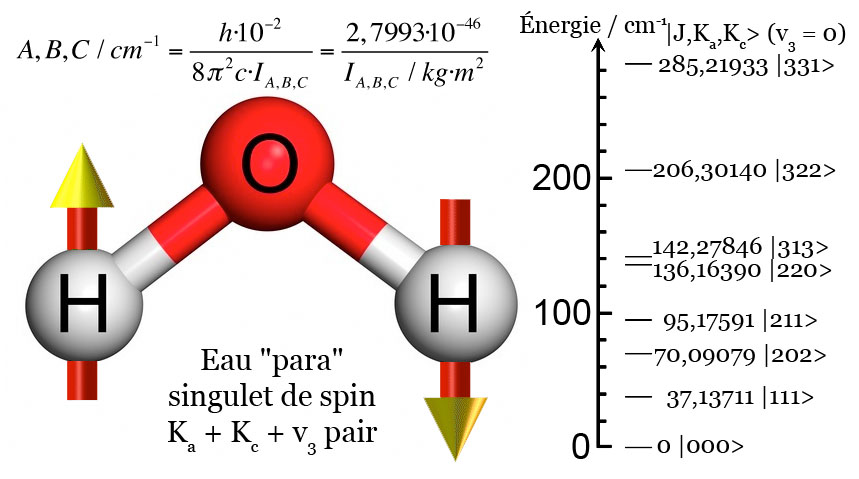
L’eau para est un isomère de spin de la molécule d’eau H₂O à l’état vapeur. Or, la molécule d’eau est une toupie asymétrique de forme ovoïde. Ses niveaux d’énergie de rotation peuvent donc être indexés à l’aide de 3 nombres quantiques |J, K_a, K_c>. Ici, J est le nombre quantique associé au moment angulaire total de rotation. Les deux nombres quantiques K_a et K_c, mesurent pour leur part les composantes du moment angulaire total J. Le premier sur l’axe principal de moindre inertie ‘a’. Le second sur celui de plus grande inertie ‘c’ :

Comme on l’a vu pour l’eau “ortho”, appliquons la permutation P₂. De manière très générale, on doit trouver :

P_{2}\mid\Gamma,v_{1},v_{2},v_{3},J,K_{a},K_{c},I> =-\mid\Gamma,v_{1},v_{2},v_{3},J,K_{a},K_{c},I>

Ceci, en raison du caractère “fermion” des deux atomes d’hydrogène. Reste à déterminer l’action de la symétrie d’échange sur la partie spin nucléaire. L’eau para étant un singulet de spin, il n’y a qu’un seul état à considérer :

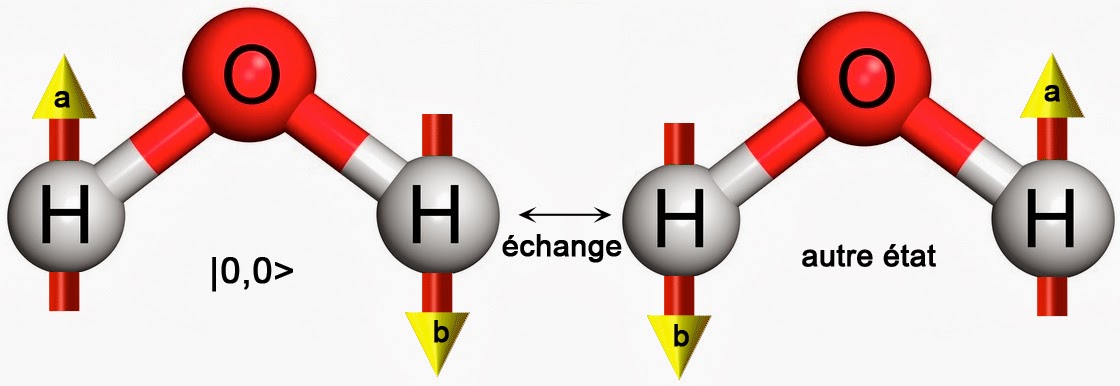
Comme dans le cas de la composante de |1,0> de l’eau “ortho”, on n’obtient pas la même situation qu’avant échange. En effet, on voit qu’avant échange, le spin de gauche pointe vers le haut. Après échange, il pointe dorénavant vers le bas. Réciproquement, le spin de droite pointant initialement vers le bas, pointe maintenant vers le haut. Ici aussi, inutile de considérer un seul état |0,0>. Il faut plutôt considérer une combinaison antisymétrique de l’état avant échange et de l’état après échange. En effet, la combinaison symétrique (signe ‘+’) a déjà été prise pour décrire l’état |1,0> de l’eau “ortho”. Il reste donc la combinaison impliquant le signe ‘-‘ :

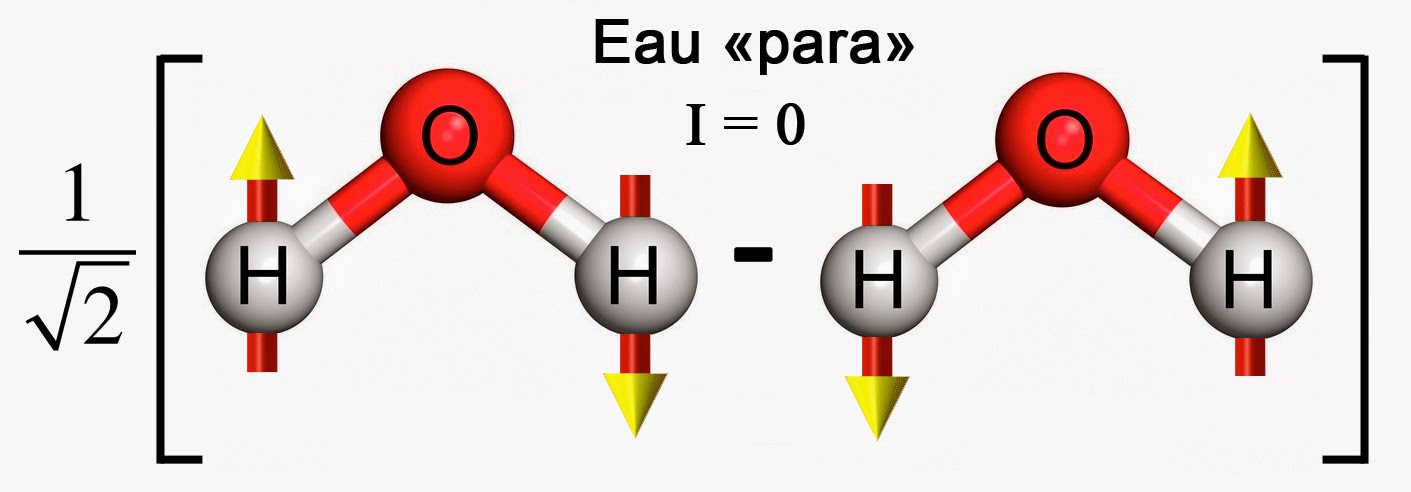
\mid 0,0> =\tfrac{1}{\sqrt{2}}\left (\mid\uparrow , \downarrow > - \mid \downarrow , \uparrow >\right )

Le facteur numérique affectant la combinaison est un facteur de normalisation. Il permet de conserver la norme de tout état quantique à la valeur 1. Avec une telle combinaison je peux maintenant faire l’échange et constater que :

P_{2}\mid 0,0> =\tfrac{1}{\sqrt{2}}\left (\mid \downarrow , \uparrow > - \mid \uparrow , \downarrow >\right)=-\mid 0,0>

On récupère ainsi bien, comme attendu, un état anti-symétrique lors de l’échange des positions des deux atomes d’hydrogène.

Parité des états quantiques

Il ne reste maintenant plus qu’à combiner ce résultat avec ce que l’on a déjà vu pour l’eau “ortho”. On obtient ainis la règle suivante :

P_{2}\mid\Gamma,v_{1},v_{2},v_{3},J,K_{a},K_{c},0>=(-1)^{v_{3}+K_{a}+K_{c}+1}\mid\Gamma,v_{1},v_{2},v_{3},J,K_{a},K_{c},0>

Plaçons-nous dans l’état de vibration |v₁, v₂, 0> où v₃ = 0. L’état quantique résultant doit toujours être antisymétrique pour l’échange de position des noyaux hydrogène. Les états rotationnels purs v₁ = v₂ = v₃ = 0 de l’eau para, où ceux impliquant les modes symétriques de vibration sont donc ceux où la somme (K_a + K_c + 1) est impaire. Ceci signifie que la somme (K_a + K_c) doit impérativement être paire. Il s’ensuit que l’eau para, contrairement à l’eau ortho, ne possède pas d’énergie rotationnelle de point zéro. Car, dans ce cas, l’état fondamental de rotation peut s’écrire |Γ,0,0,0,0,0,0,0>. Ou plus simplement |0,0,0>_para, avec K_a = K_c = 0. En effet, 0 est le plus petit nombre entier pair.

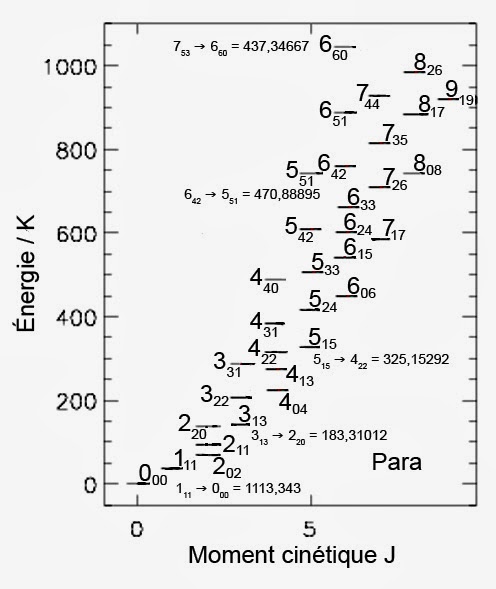
Par conséquent, l’eau para peut s’arrêter de tournoyer autour de son centre de masse. Ceci, à température ambiante et en l’absence de rayonnement infrarouge pouvant exciter la molécule dès que la température devient inférieure à T = 50K. La figure ci-dessous montre les niveaux d’énergie purement rotationnels de l’eau para, avec quelques transitions couramment observées en milieu interstellaire :