Dans le cadre de la gravitation quantique, vide et matière sont deux concepts interchangeables. Ceci peut paraître, à première vue, assez surprenant… Voyons comment cela est possible. Selon la théorie de la relativité générale, la plus grande masse m qui puisse être mise dans une boîte de taille R est un trou noir ayant un rayon de Schwarzschild R_S de même valeur :

Mati\grave{e} re  \Rightarrow R \geqslant {R_S} = \frac{{2G\cdot m}}{{{c^2}}} \Rightarrow m \leqslant \frac{{R\cdot{c^2}}}{G}

Ici, G = 6,67·10^-11 J·m·kg^-2 désigne la constante de gravitation universelle et c = 3·10⁸ m·s^-1 la vitesse de déplacement de la lumière dans le vide. D’autre part, selon la physique quantique, la plus petite masse présente dans une telle boîte, correspondant à ce que nous appelons du vide, provient des relations d’incertitudes d’Heisenberg. Ainsi, à toute masse m correspond une longueur d’onde de Compton λ_C. Cette dernière représente la taille minimale R pouvant contenir une telle masse :

Vide \Rightarrow R\geqslant \lambda_{C} = \dfrac{\hbar}{m\cdot c}\Rightarrow m\geqslant \frac{\hbar}{c\cdot R}

Ici, ℏ = 1,06·10^-34 J·s désigne la constante réduite de Planck. Par conséquent, à l’intérieur de toute boîte de taille R, on ne peut trouver qu’une masse m, qui est encadrée par les valeurs suivantes :

\dfrac{\hbar}{c\cdot R}\leqslant m\leqslant \dfrac{c^{2}\cdot R}{G}

Longueur de Planck

Voyons ce que donne cette inégalité fondamentale dans le cas d’un être humain ayant une taille de 1m,80 et faisant 80 kg.

2,0\cdot 10^{-43} kg\leqslant 80 kg\leqslant 2,4\cdot 10^{27} kg

Comme on peut le voir, il y a de la marge aussi bien vers le bas que vers le haut. À cette échelle dite “macroscopique” la différence entre vide et matière est évidente. Par conséquent, il est difficile de confondre les deux. Considérons maintenant la plus petite masse de matière de rayon connue qui est le proton, avec une masse m = 1,7·10^-27 kg pour un rayon de 1 fm = 10^-15 m. Si l’on refait le même calcul, il vient :

3,5\cdot 10^{-28} kg \leqslant 1,7\cdot 10^{-27} kg\leqslant 1,4\cdot 10^{12} kg

On voit que l’écart s’est considérablement réduit. Ce qu’il est important de constater c’est que les deux quantités de part et d’autre de la masse sont finies. Il en découle l’existence d’une certaine taille, dite longueur de Planck, où la limite de masse à droite devient égale à la limite de masse à gauche :

\dfrac{\hbar}{c\cdot R}=\dfrac{c^{2}\cdot R}{G}\Rightarrow L_{Pl}=\sqrt{\dfrac{\hbar\cdot G}{c^{3}}}\approx 2,6\cdot 10^{-34} m

Peser le vide…

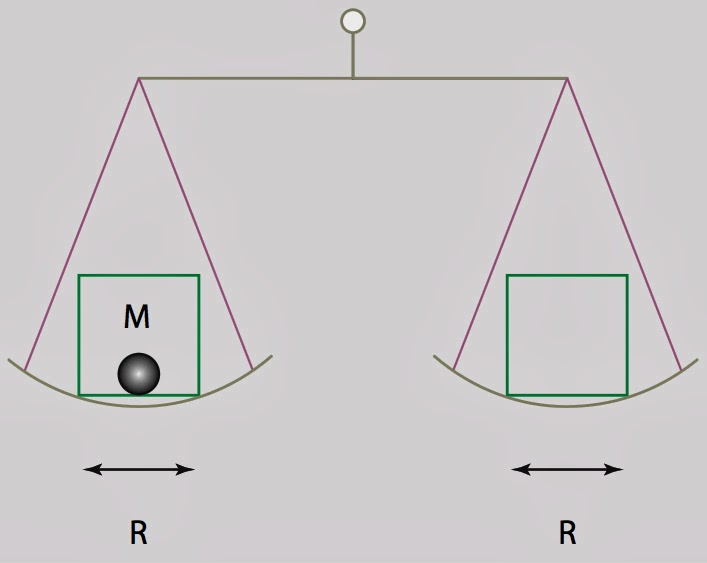
Autrement dit, si l’on construit une balance avec deux boîtes de la taille de Planck, l’une vide et l’autre pleine, il sera impossible de décider de quel côté penchera la balance ! En effet, même si l’on répète un grand nombre de fois la mesure, la balance s’inclinera d’un côté ou de l’autre au hasard et restera donc en moyenne parfaitement horizontale.

On peut traduire ces résultats d’une autre manière. D’un côté, si l’on mesure la masse d’une région vide de taille R, le résultat sera toujours au moins ħ/cR. Car, aucun vide parfait n’existe dans la nature en raison des lois de la physique quantique. D’autre part, si nous mesurons la masse d’une particule, on trouvera que le résultat dépend de la taille. Car, à l’échelle de Planck, on trouvera toujours la masse de Planck pour tout type de particule. Qu’il s’agisse de matière ou de rayonnement.

Utilisons une autre image. Soit deux particules qui s’approchent l’une de l’autre jusqu’à être séparées par une distance de l’ordre de la longueur de Planck. Alors, l’incertitude sur la mesure de la distance fait qu’il est impossible de savoir s’il y a quelque chose ou rien entre les deux objets. En résumé, les notions de matière et de vide sont interchangeables à l’échelle de Planck.

Effet Fulling-Davies-Unruh

Ceci est un résultat très important. En effet, la masse et l’espace vide ne peuvent être différenciés. Cela signifie qu’ils sont faits de la même chose, des mêmes constituants. Ceci est aussi corroboré par les tentatives d’appliquer la physique quantique à l’espace-temps très fortement courbé. Ici, il devient impossible de faire une distinction claire entre vide et particules, comme le démontre l’effet Fulling-Davies-Unruh. Cet effet fut découvert de manière indépendante par Stephen Fulling en 1973, Paul Davies en 1975 et William Unruh en 1976. Il stipule que si un observateur inertiel observe qu’il est entouré de vide, un autre observateur accéléré par rapport au premier ne voit pas du vide, mais une radiation présentant un spectre du corps noir avec une température T donnée par :

T=a\cdot\frac{\hbar}{2\pi k_{B}\cdot c}

Ici, a est la valeur de l’accélération et k_B = 1,38·10^-23 J·K^-1, la constante de Boltzmann. Ce résultat implique en particulier que le vide n’existe pas sur Terre. Car, tout observateur terrestre à la surface de la Terre subit une accélération de 9,8 m·s^-2. Or, ceci correspondant à une température T = 40 zK ! Il est donc théoriquement possible de mesurer la gravité avec un simple thermomètre. Hélas, même pour les plus fortes accélérations connues, les valeurs de températures sont extrêmement petites. Ceci rend la mesure expérimentale extraordinairement difficile. Cet effet se produit également pour un observateur ayant un mouvement de rotation. Dans ce cas, on a pu également montrer que la simple accélération d’un miroir conduisait à l’émission de la radiation Unruh. Il est donc plus difficile d’accélérer les miroirs que des corps non réfléchissant de même masse.

Masse = espace-temps

Si l’accélération devient suffisamment élevée, il est également possible que des particules de matière soit émises et détectées. Autrement dit, si l’on accélère un compteur Geiger de manière suffisante dans le vide, il commencera à compter des particules ! La différence entre vide et matière devient donc bien floue pour de très grandes accélérations. Il en sera de même pour un espace-temps courbé. L’idée que le vide soit vu comme un milieu exempt de particules ne fonctionne pas. Puisqu’à l’échelle de Planck, il est impossible de dire si l’espace est plat. Il est également impossible de dire s’il contient des particules ou pas. On retrouve donc bien la parfaite équivalence entre vide et matière.

Pour résumer, tous les arguments arrivent à la même conclusion : le vide spatio-temporel ne peut pas être distingué de la matière à l’échelle de Planck. Il y a un autre moyen d’exprimer cela. C’est de dire que si une particule ayant l’énergie de Planck se déplace dans l’espace, elle sera diffusée par les fluctuations de l’espace-temps lui-même. Aussi bien que par la matière rencontrée. Les deux cas ne sont pas distinguables sur un plan expérimental. Ces résultats très surprenants reposent sur un fait très simple. Quelle que soit la définition de la masse que l’on utilise, il faudra toujours faire appel à des mesures combinées d’espace et de temps. Ceci est vrai même pour les balances à plateaux, où la masse est mesurée par le déplacement d’une pièce mobile de la machine.

L’échelle de Planck

La mesure des masses est donc impossible aux échelles de Planck. Car, les erreurs faites lors de ces mesures font qu’il est impossible de distinguer entre vide et matière. En particulier, le concept même de particule n’est plus pertinent à l’échelle de Planck. Par-dessus tout, il n’existe ni matière, ni rayonnement, ni horizon, ni espace, ni temps à l’échelle de Planck. Tous ces concepts ne sont pertinents que dans des situations de faible énergie. Or, les observateurs sont faits de matière et non de rayonnement, ni de vide. La notion d’observateur est donc biaisée par un point de vue très particulier. Il en découle que les observateurs n’existent plus au voisinage de l’énergie de Planck. Car, il ne peut plus avoir de biais en faveur de la matière par rapport au vide. La physique moderne n’est donc pertinente qu’en dessous de l’énergie de Planck.

On apporte ainsi une nouvelle réponse à une question très ancienne : « pourquoi existe-t-il quelque chose plutôt que rien » ? A l’échelle de Planck, la réponse est triviale : il n’existe aucune différence entre quelque chose et rien. C’est-à-dire qu’en toute honnêteté, nous pouvons dire que nous sommes faits de rien. L’impossibilité de distinguer entre la matière et le vide implique l’absence d’information à l’échelle de Planck. Par ricochet, cela implique l’existence d’une entropie de base associée à toute partie de l’univers. Tout ceci amène bien sûr à la question de savoir à partir de quelle énergie il devient possible de distinguer la matière du vide.

Conclusion

Une réponse peut être donnée en posant une autre question : peut-on distinguer un liquide d’un gaz en regardant un seul atome ? Non, bien sûr, pour cela il faut considérer beaucoup d’atomes. De même, il est impossible de distinguer entre vide et matière en ne regardant qu’un seul point de l’espace-temps. Il faut pour cela considérer un très grand nombre de points. Tout ce que nous pouvons observer, ce sont des moyennes. Cependant, il n’existe aucune moyenne parfaite. Chercher à distinguer la matière du vide, c’est un peu comme chercher à distinguer les nuages dans un ciel clair. A l’instar des nuages, la matière ne possède pas de frontière précise.

Enfin, puisque vide, particules et champs ne peuvent être distingués à l’échelle de Planck, nous perdons aussi la distinction entre états transitoires et permanents. Ainsi que toutes les propriétés intrinsèques des systèmes physiques. Ceci est un résultat très fort. Puisque cela signifie qu’il est impossible de distinguer un système de son environnement. Autrement dit, à l’échelle de Planck, le mouvement n’existe plus.