Introduction

Les musiques que je produis en collaboration avec Tommi Jack’s sont toutes au diapason de l’eau (fréquence de 429,62 Hz). Mais, derrière cette affirmation, bien peu de personnes semblent comprendre en quoi consiste réellement le travail effectué. Or, derrière ce travail se trouve l’idée que notre univers observable est avant tout de nature vibratoire, plutôt que fait de matière. Car, une telle dualité entre matière et vibration se doit d’être bien comprise pour comprendre l’effet que peut avoir une musique sur une matière vivante.

Ainsi, je me suis permis de lancer sur Facebook et sur X (ex-Twitter) une série en 12 épisodes. Et, comme tout le monde n’a pas accès aux réseaux sociaux, je regroupe ici ces 12 épisodes en quelques chroniques. Chacune et chacun pourra, à tout moment, de cette façon revenir sur ces épisodes sans avoir à se connecter sur un réseau particulier. Car, l’on sait pertinemment que l’information sur ces réseaux peut être supprimée à tout instant. Ceci, selon les caprices d’un milliardaire comme Mark Zuckerberg (PDG de Facebook) ou Elon Musk (PDG de X Corp.). D’où la nécessité de protéger cette information de manière indépendante.

“Tout est fréquence…”

Le premier point est cette phrase absolument débile selon laquelle chaque atome, chaque molécule, chaque être vivant, chaque pensée, chaque émotion, vibre à une certaine fréquence. Et, que l’ensemble de ces fréquences crée l’univers que nous connaissons. Or, rien n’est plus faux. Tous ceux et toutes celles qui propagent ce genre de raisonnement font preuve d’une ignorance totale de ce qu’est vraiment une vibration. Parce que la véritable assertion serait plutôt que : « chaque atome, chaque molécule, chaque être vivant, chaque pensée, chaque émotion, correspond à une vibration. » Là, on est dans le réel et non dans le fantasme. De fait, réduire une vibration à sa simple fréquence est un piège qui vient de notre éducation.

Pour faire simple, on apprend dès la maternelle qu’il existe une notion appelée « matière ». Et, que pour mesurer la quantité de matière, on doit mesurer la masse. Puis, arrive la physique quantique qui affirme que la matière n’existe pas et que ce serait une vibration influençable par la pensée (expérience des deux fentes). Là, on n’est plus à la maternelle, mais en université. Mais, cette pensée, fortement enracinée dans la matière dès notre plus jeune âge, nous oblige à chercher, ce qui, dans une vibration, est équivalent à une masse.

Et, là, se referme le piège redoutable : pour un grand nombre de béotiens, une vibration se caractériserait par sa fréquence. Toutefois, voilà, alors qu’une matière se caractérise par sa masse et rien d’autre, une vibration s’exprime selon quatre modalités : une fréquence, une longueur d’onde, une amplitude et surtout une phase. Si vous ne prenez pas en compte ces quatre notions de manière simultanée, vous ne comprendrez jamais ce qu’est une vibration.

Tout est vibration

Par conséquent, si l’on souhaite être clair, dans l’univers tout vibre. Mais, cela ne veut en aucune manière dire que tout est fréquence. Saisissez-vous bien la nuance ? Si la réponse est « non », inutile d’aller plus loin. Mais, si la réponse est « oui », alors, bienvenue dans le monde des musiques au diapason de l’eau. Allez, je vais me répéter. Néanmoins, tant pis. Une masse, cela se mesure en kilogrammes (kg) pour la mécanique. Toutefois, une telle masse de matière correspond à un nombre de moles pour la chimie et les sciences qui en dérivent : biologie et médecine.

D’où mon insistance à dire qu’une cellule, c’est 996 mol‰ d’eau salée, alors que ce chiffre devient 986 mol‰ pour un homme et 983 mol‰ pour une femme. Cherchez bien sur Internet et vous ne verrez jamais ces chiffres. Sauf dans mes écrits et dans mes publications. Car, nul besoin d’avoir fait polytechnique pour comprendre que toute maladie est avant tout un problème d’eau salée et que tout remède est, lui aussi, à la base, une affaire d’eau salée. Tout le reste, c’est-à-dire tout ce que vous voyez dans le miroir, c’est « cacahuètes ». Tout cela n’existe que parce que derrière, tout repose sur de l’eau salée. Le chimiste Gerald Pollack, aime, lui, à parler du « quatrième état de l’eau ». Alors que votre serviteur préfère parler « d’eau morphogénique ». Car, techniquement parlant, l’eau salée n’est pas de l’eau.
Passons maintenant à la vibration. Ici, ce n’est pas une unité qu’il faut, mais plusieurs.

Unités de mesure pour une vibration

Parce que, sur les quatre attributs de la vibration, trois n’ont qu’une seule unité :

– Le hertz ou nombre d’oscillations par unité de temps (s^-1) pour la fréquence f.
– Le mètre (m) ou nombre d’oscillations par unité de longueur pour la longueur d’onde λ.
– Le radian (rad) pour l’angle de phase 𝜑 variant de 0 à 2π rad (360°).

L’unité de mesure pour le quatrième attribut de la vibration, l’amplitude, elle dépend du type de vibration considéré. Cela peut être une accélération pour une vibration mécanique (m·s^-2). Ou bien alors à un champ électrique (V·m^-1) pour une vibration électrique. Ou bien encore, une densité de flux magnétique (T) pour une vibration magnétique. Mais, également, une intensité pour une onde électromagnétique.
Peut-être, commencez-vous à percevoir, pourquoi la vibration est un concept beaucoup plus riche et complexe que le concept de matière… Et, que réduire cette complexité à la seule variation temporelle (fréquence) est une faute grave qu’il convient d’éviter à tout prix.

Équivalence entre masse molaire et fréquence

Par conséquent, il devrait être dorénavant bien clair qu’une vibration ne peut pas être réduite à sa seule fréquence. Il est aussi vrai que toute matière peut être vue comme une vibration. Ceci enrichit considérablement la vision que l’on peut avoir de cette matière. Cette dernière devient autre chose qu’une masse inertielle (résistance au mouvement) ou qu’une masse gravitationnelle (force d’attraction). Masse inertielle ou gravitationnelle qui, quoi qu’il arrive, ont toujours la même valeur numérique, appelée “masse”. Prenons maintenant notre molécule d’eau dont la masse molaire est bien connue (M = 18,01528 Da). Dans deux publications scientifiques, nous avons proposé qu’une telle masse corresponde à une vibration de fréquence f = 429,62 Hz [1][2]. Ceci, grâce à la relation de De Broglie-Sternheimer : f (Hz) = 2³×2,980951×M(Da).

Vibration, matière et taille humaine

Ceci étant acquis, nous savons également qu’à cette fréquence f correspond une certaine longueur d’onde λ. Cette dernière est calculable au moyen de la relation : λ×f = v. Ici, v est la vitesse de propagation de l’onde sonore. Or, la vitesse pertinente est celle de la propagation du son dans de l’eau salée à une température T = 37°C. Pour une salinité moyenne entre hommes et femmes de 10‰, on trouve une vitesse v = 1534 m·s^-1 [3].

Dans ces conditions, une fréquence sonore de 429,62 Hz correspond, pour un être humain, à une longueur d’onde λ = 1534/429,62 = 3,57 m. Valeur à comparer à la taille moyenne d’un homme (h = 1,75 m) ou d’une femme (h = 1,62 m). On constate donc que l’onde sonore affecte le corps dans son ensemble (λ > h). Mais, également tout ce qui se trouve à environ 1 m de ce dernier.

Vibration, matière et piézoélectricité

Ceci étant établi, nous avons ignoré la matière anhydre biologique qui compose ce corps humain. Or, il se trouve que cette matière a la propriété d’être chirale. C’est-à-dire apte à faire la différence entre la droite et la gauche. Or, toute matière disposant de la faculté de chiralité, possède un tenseur piézoélectrique non nul. Propriété qui assure que toute pression sonore peut être transformée en charges électriques. Et, selon les équations de Maxwell, toute variation périodique de charges électriques entraîne une émission de vibrations de nature électromagnétique se propageant à une vitesse c = 299 792 458 m·s^-1.

Considérons cette piézoélectricité du corps humain. Alors, la même fréquence de 429,62 Hz correspond à une nouvelle longueur d’onde λ = 299 792 458/429,62 = 697 808 m. Soit environ 700 km. On a donc complètement changé d’échelle. Avec une sensibilité de ce même corps humain à la musique écoutée. Mais, également, à toutes les influences électromagnétiques qui se trouvent dans un rayon de 700 km autour de ce corps…

Connexion avec toute forme de vie

Tout ceci nous montre bien la complexité qui se cache derrière une valeur telle que 429,62 Hz de fréquence. Si l’on oublie l’aspect longueur d’onde, on pense écouter une musique provenant d’une source proche de quelques mètres. Alors, qu’en réalité, cette source sonore est modulée par tout ce qui passe dans un rayon d’environ 700 km… Il vaut mieux en être conscient.

Évidemment, ceci n’est pas spécifique au diapason de l’eau, mais s’applique à tout diapason. Néanmoins, si vous utilisez un autre diapason, vous n’êtes connectés qu’avec ce qui est inerte et dénué de vie. Or, l’eau, c’est la vie… Et, donc, en écoutant une musique au diapason de l’eau, on se connecte, par résonance, à toute matière se trouvant dans un rayon de 700 km autour de vous. Mais, aussi, à toute forme de vie se trouvant dans ce même rayon : bactéries, plantes, animaux et autres êtres humains. D’où l’originalité de ce diapason de l’eau par rapport à un autre diapason. Toutefois, vous n’aurez pas nécessairement le même ressenti à chaque écoute. En effet, bien sûr, entre deux écoutes, le milieu vivant environnant dans un rayon de 700 km a totalement évolué.

Par conséquent, écouter une musique accordée au diapason de l’eau est une expérience unique à chaque écoute. Il convient de bien avoir conscience de cela, au lieu de penser bêtement que vous écoutez toujours la même musique.

Amplitude et phase vibratoire

Nous savons maintenant faire la différence entre l’idée que « tout est fait de matière » et l’idée que « tout est vibration ». Supposons que tout soit fait de matière. Alors, ce qui compte, c’est soit le nombre de particules N (chimie, biologie, médecine), soit la masse M (mécanique, astronomie). Cependant, on peut aussi supposer que tout est vibration. Alors, il existe quatre manières de voir le monde qui nous entoure. Par la fréquence f, par la longueur d’onde λ, par l’amplitude A ou par la phase 𝞿.

Nous savons aussi, à ce stade, qu’à une même fréquence f, peuvent correspondre plusieurs longueurs d’onde. Ceci, selon la nature de la vibration : mécanique ou électromagnétique. Dans cette section, nous allons nous intéresser aux deux derniers paramètres : l’amplitude A et la phase 𝞿. Ici, impossible de dissocier les deux.

Phaser une vibration

La première chose à savoir est que, sur un plan purement matériel, la somme 1 + 1 vaut toujours 2, et rien d’autre. Cependant, sur un plan vibratoire, cette même somme 1 + 1 peut prendre n’importe quelle valeur de 1 à 4. Pire, on peut même avoir 1 + 1 = 0. Cette spécificité tient au fait que dès que l’on additionne deux vibrations, le résultat dépend du différentiel de phase ∆𝞿 existant entre les deux vibrations. Car, une vibration présente la propriété de se reproduire égale à elle-même après une oscillation temporelle (fréquence) ou bien après une oscillation spatiale (longueur d’onde).

Dans ces conditions, phaser une vibration revient à préciser une origine temporelle, ou bien une origine spatiale où l’amplitude de la vibration s’annule : A = 0. Et, tant que l’on affaire à une seule vibration, ce choix d’origine importe peu. Toutefois, dès qu’il existe un minimum de deux vibrations, se pose un problème. Car, une fois l’origine temporelle ou spatiale choisie, impossible d’en changer. Parce que, l’origine ne peut être qu’unique, quel que soit le nombre de vibrations considérées.

Interférences constructives et destructives

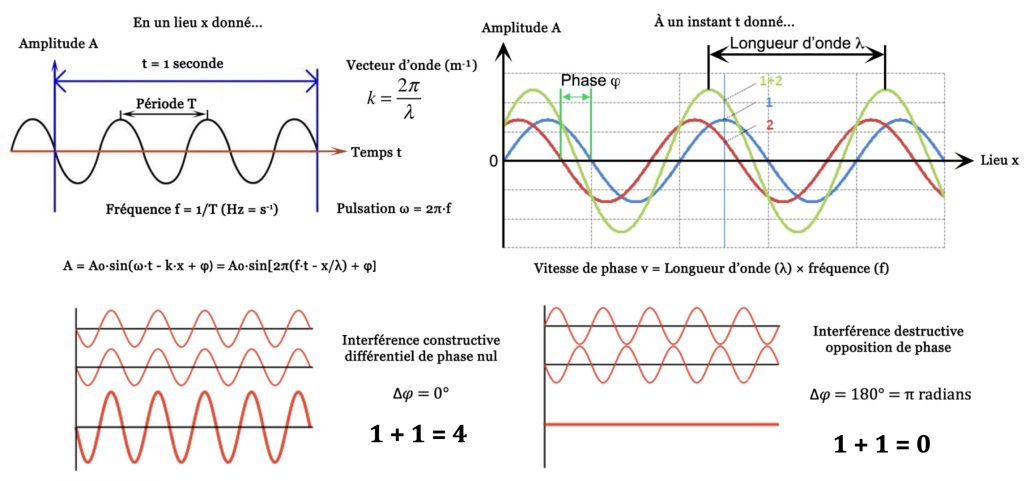
Pour aller plus loin, le plus simple est de se limiter à la superposition de deux vibrations. Comme le montre la figure ci-dessus, une première possibilité est que les deux vibrations aient la même amplitude. Ceci à un moment donné et dans un lieu donné. Dans ce cas, on dit que leur différentiel de phase est nul : ∆𝞿 = 0°. Conséquence, les deux vibrations sont dites “en phase” et la somme des deux amplitudes A + A = 2×A est le double de l’amplitude A de chaque vibration. Et, comme l’intensité est donnée par le carré de l’amplitude, on a (A + A)² = (2A)² = 4 A². Soit, si l’on compare au cas où les deux vibrations seraient indépendantes : A² + A² = 4×A², soit 1 + 1 = 4.

Mais, il y a aussi une seconde possibilité. Celle où les deux vibrations sont en opposition de phase : ∆𝞿 = 180°. Autrement dit, que pour l’origine choisie, la première vibration prend sa valeur maximale +A, alors que la seconde vibration prend sa valeur minimale : -A. Et, donc, dans ce cas, la superposition des deux vibrations donne (A – A)² = 0² = 0. Soit, par rapport au cas où les deux vibrations seraient indépendantes : A² + A² = 0×A², soit 1 + 1 = 0. C’est précisément ici que l’on peut comprendre la raison pour laquelle, en physique vibratoire, une chose peut être vide, puisque au final, on ne voit rien (0), alors que pourtant, il y a bien deux vibrations (1 – 1), mais inobservables.

Phase, information et nombre complexe

Autrement dit, cette notion de phase joue un rôle crucial, alors qu’elle est, par principe, inobservable. Seul compte pour l’observation, le différentiel de phase ∆𝞿 et non la phase elle-même. Mais, cela va encore plus loin. Parce que l’on sait que toute vibration peut apporter une information. Et, que cette information peut être codée, soit via la fréquence (modulation de fréquence), soit via la phase (modulation d’amplitude). Or, la vie, afin de transmettre l’information, code cette dernière sur les phases. La fréquence n’intervient que pour assurer qu’il existe bien une résonance entre l’émetteur et le récepteur.

Notons ici que tout ceci s’applique à tout type de vibration, qu’elle soit mécanique (sonore), électromagnétique ou quantique. Sachez aussi, que, sur un plan mathématique, jouer avec la phase revient à abandonner la notion de nombre réel. Ceci pour utiliser, à la place, la notion de nombre complexe, avec une partie réelle A·cos 𝞿 et une partie imaginaire A·sin 𝞿. D’où le fait que la phase 𝞿 peut être vue comme un angle prenant toute valeur de 0 à 2π radians (soit de 0 à 360°). Dans ces conditions, additionner plusieurs vibrations de même fréquence, mais déphasées les unes par rapport aux autres, revient à additionner des nombres complexes. Ceci explique la différence avec la matière où l’on additionne simplement des nombres réels.

Références

[1] Henry, M., Bridoux, S. (2024). “Symmetry, Music and Water”. J Human. Soc. Sci., 7(4), 01-25.
https://www.opastpublishers.com/open-access-articles/symmetry-music-and-water.pdf
[2] Henry, M. (2024), “Water and the origin of life”, Water (MDPI), 16, 2854.
https://www.mdpi.com/2073-4441/16/19/2854
[3] Chen‐Tung Chen; Frank J. Millero (1977), “Speed of sound in seawater at high pressures”, J. Acoust. Soc. Am., 62, 1129–1135.
https://doi.org/10.1121/1.381646