Thermomètres

 L’invention du thermomètre fut une étape décisive permettant d’associer un nombre à un état thermique donné. Ce thermomètre peut être formé d’une colonne de mercure de hauteur variable. Il peut aussi s’agir d’une bilame métallique se déplaçant le long d’une échelle graduée. Il est fort probable que les thermomètres furent utilisés dès la plus haute antiquité. Toutefois, la première personne ayant rapporté l’emploi d’un tel instrument dans le but de réaliser des expériences fut Galilée en 1592.

Galilée remarqua que la densité d’un liquide variait avec la température. Il imagina alors un cylindre de verre scellé rempli d’un liquide transparent. Ce cylindre pouvait contenir une série d’objets de densités différentes. Au fur et à mesure que le liquide dans lequel ils baignent s’échauffe, ils peuvent couler un par un. On peut aussi fabriquer des thermomètres en se basant sur le fait qu’un liquide change de volume avec la température.

Notion d’équilibre thermique

À ce stade, on doit utiliser la lettre grecque θ pour de tels thermomètres. Il s’agit essentiellement d’une température empirique qui est complètement arbitraire. En effet, l’absence de calibrage fait que n’importe quelle fonction monotone et croissante θ’ = f(θ) peut être employée pour définir une autre échelle de température.

Maintenant, plaçons de l’eau chaude et de l’eau froide dans un volume clos isolé thermiquement de l’extérieur. On observera alors que l’eau chaude va se refroidir et que l’eau froide va se réchauffer. Après un temps plus ou moins long, les propriétés macroscopiques mesurables de ce système ne varieront plus. Sauf si un facteur extérieur vient perturber l’état atteint. Lorsqu’un tel état stationnaire est atteint on parle d’état d’équilibre. Un cas particulier d’équilibre est rencontré lorsqu’un thermomètre est placé au contact d’un autre corps :

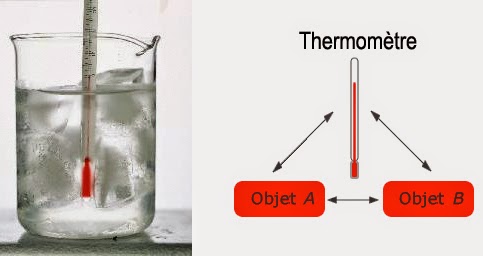
La valeur θ affichée par le thermomètre peut très bien fluctuer au premier abord. Mais, elle finira par atteindre, au bout d’un certain temps, un état stationnaire. Quand le nombre θ devient constant dans le temps, on dit que le thermomètre est en équilibre thermique avec son environnement. Et, par extension, on dit que son environnement se trouve à la température θ. 

Raisonner par induction

Soit donc deux corps présentant la même température. Ceci signifie qu’un thermomètre affiche la même valeur quand on le met en contact avec l’un ou l’autre de ces deux corps. Soit aussi la proposition « ces deux corps possèdent la même température ». On veut, bien évidemment, qu’une telle proposition ne soit pas un simple artefact lié au type de thermomètre utilisé. Il est donc absolument nécessaire que ceci soit vrai pour tous les thermomètres sans exception. Et, en ce domaine, seule l’expérience est compétente pour vérifier cette propriété d’universalité.

Or, il n’existe aucune évidence positive pour que tous les thermomètres affichent la même température. De même, il n’existe également aucune évidence négative contre cette proposition. Posons-nous maintenant la question de savoir si lorsque deux corps sont à la même température, ils sont aussi nécessairement en équilibre thermique. De nouveau, seul le recours à l’expérience permet de savoir si cette proposition est vraie ou fausse. Et, la conclusion générale est ici aussi plus supportée par l’absence d’évidence négative que par une évidence positive spécifique.

Principe zéro de la thermodynamique

Ce type de raisonnement par induction a été critiqué sur le plan strictement logique via le paradoxe des corbeaux proposé par le logicien Carl Gustav Hempel (1905-1997). On admettra donc comme principe zéro de la thermodynamique que l’équilibre possède la propriété générale suivante : « deux corps en équilibre avec un troisième, sont également en équilibre entre eux ». Ceci est un fait empirique non démontrable, mais néanmoins très plausible :

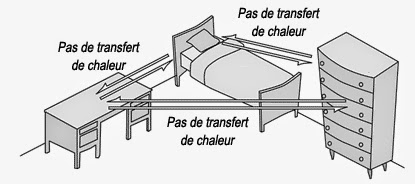
Or, je suis libre de choisir que le troisième corps en question soit un thermomètre. Ce principe zéro peut aussi s’énoncer de la manière suivante : « deux corps sont en équilibre thermique entre eux s’ils possèdent la même température ». On notera toutefois que ce deuxième énoncé a une portée plus restreinte que le premier. Car, en relativité générale, le premier énoncé est vrai alors que second est faux.

En effet, en présence d’un potentiel gravitationnel φ, l’état d’équilibre ne requiert pas que la température soit uniforme en tout point. Mais, plutôt que la fonction T·exp(φ/c²) soit constante. Bien évidemment, pour des champs de gravitation faibles, le terme exp(φ/c²) est très proche de l’unité. Dans ces conditions, c’est bien l’uniformité de la température qui définit l’état d’équilibre. 

États hors équilibre

Ceci nous montre très clairement que la thermodynamique est une science des états d’équilibre. Car, la notion même de température ne peut être parfaitement définie que lorsqu’on se trouve dans un état d’équilibre. En conséquence, le concept de température variable dans le temps n’a en soi aucun sens en thermodynamique. Ceci ne veut pas dire bien sûr qu’il est impossible d’étudier des états où la température varie dans le temps. Mais, simplement que la compréhension de tels états sera beaucoup plus complexe que celle des états d’équilibre.

Vouloir comprendre un système hors équilibre sans connaître les lois des systèmes à l’équilibre, c’est un peu comme se jeter à l’eau sans bouée lorsqu’on ne sait pas nager…

Premières échelles de température

Vers 1700, Isaac Newton s’intéressa au problème de la chaleur. Il constata ainsi que la plupart des substances se dilatent en se réchauffant. Il mesura ainsi le changement de volume de l’huile de lin. Ce, pour une vingtaine de points de référence allant de « l’air froid en hiver » jusqu’aux « charbons ardents du feu de cuisine ». Il observa ainsi qu’un litre d’huile de lin à la température de la neige fondante atteignait 1,0725 litre à la température de l’eau bouillante. Au bout d’un certain temps, il définit le « zéro degré de chaleur » comme correspondant à la neige fondante. Puis, de manière très arbitraire le « 33 degrés de chaleur » comme correspondant à l’eau bouillante. Il baptisa son instrument un « thermomètre ».

Le travail de Newton fut repris par l’astronome Danois Ole Christensen Rømer. Ce dernier proposa, en1701, une autre échelle de température. Ici, le zéro correspondait au point de congélation d’une saumure d’eau, de glace et de chlorure d’ammonium. Sur cette échelle, le point d’ébullition de l’eau était fixé de manière arbitraire à 60°. Il constata alors que le point de congélation de l’eau ordinaire non salée tombait aux alentours du huitième de cette valeur (soit 7,5 degrés). Il décida donc d’utiliser cette valeur comme second point fixe.  Avec cette échelle complètement arbitraire l’eau congèle à 7,5°Ro et bout à 60°Ro. 

Degrés Fahrenheit et Réaumur

Ayant visité le laboratoire de Rømer, le physicien allemand Gabriel Fahrenheit introduisit dès 1724 le degré Fahrenheit (symbole °F). Sa référence basse était le point de solidification d’un mélange fait d’un volume égal de chlorure d’ammonium et d’eau (θ = 0°F). Ceci correspondait approximativement à la température la plus basse qu’il ait mesurée durant le rude hiver de 1709 dans la ville de Danzig. Puis, il prit acte de la valeur de 7,5°Ro pour le point de congélation de l’eau non salée, qu’il arrondit à 8°Ro. Il constata alors que pour atteindre la température du sang d’un cheval, il lui fallait appliquer 12 fois cet écart, soit θ = 12×8 = 96°F. Avec cette nouvelle échelle tout aussi arbitraire que les précédentes l’eau congèle à 32°F et bout à 212°F. 

En 1731, le physicien français René-Antoine Ferchault de Réaumur introduisit le degré Réaumur (symbole °Re). Son idée fut de se baser sur la dilatation apparente de l’alcool. Il calibra ainsi un intervalle de référence entre le point de congélation de l’eau (θ = 0°Re) et son point d’ébullition θ = 80°Re. 

Le degré Delisle

En 1732, l’astronome français Joseph-Nicolas Delisle fut invité à travailler en Russie par Pierre le Grand. Il profita de son séjour pour fabriquer des thermomètres au mercure. Son point de référence était le point d’ébullition de l’eau non salée. Il mesurait alors la contraction du mercure en cent-millièmes, suite à une baisse de température. C’est la raison pour laquelle les thermomètres Delisle comptaient en général 2 400 graduations. Ceci était approprié pour les rudes hivers de Saint-Pétersbourg. 

En 1738, le physicien allemand Josias Weitbrecht (1702–1747) recalibra l’échelle Delisle en fixant à 150 degrés le point de congélation de l’eau. Avec cette échelle, “inversée” par rapport aux autres, l’eau congèle à 150°D et bout à 0°D. L’avantage de l’échelle de Delisle est qu’elle évite les températures négatives dans le contexte de la vie quotidienne en Russie.

Le degré Celsius ou centigrade

L’astronome suédois Anders Celsius introduisit pour sa part le degré centigrade en 1742. Il choisit comme point zéro le point d’ébullition de l’eau ordinaire et en fixant de manière arbitraire le point de congélation de l’eau à 100°C. L’échelle centigrade de Celsius était donc à l’origine une échelle inversée comme celle de Delisle. Ceci permettait d’éviter l’emploi de températures négatives. Elle fut inversée vers 1744 après la mort de l’inventeur par des fabricants de thermomètre suédois comme Martin Strömer ou Daniel Ekström. Suite à cette inversion, l’eau congèle à θ = 0°C et bout à θ = 100°C.

Température absolue

Au XIXᵉ siècle toutes ces échelles empiriques et arbitraires furent remplacées par la notion de température absolue. L’idée de base est que le phénomène physique fondamental qui sous-tend la notion de température est l’agitation des particules constituant la matière. Son point origine, ou zéro absolu, correspond à l’état de la matière où ces particules ont une agitation minimale. Dans cet état, les molécules ne peuvent plus être refroidies. Autrement dit, la température traduit l’énergie cinétique des constituants de la matière que sont les atomes et les molécules.

Le premier à avoir introduit cette notion en 1848  fut William Thomson devenu plus tard Lord Kelvin. Pour cela il choisit de faire coïncider son échelle absolue avec celle des degrés centigrades de Celsius. Pour sa part, William Rankine préféra en 1859 utiliser l’échelle de Fahrenheit. En 1948, on introduisit le degré Celsius (symbole °C) en imposant que la température du point triple de l’eau où coexistent les trois phases solide, liquide et vapeur soit exactement égal à 0,01°C, ce qui place le zéro absolu à -273,15 °C. Le point d‘ébullition de l’eau à pression atmosphérique se trouve alors à 99,975°C. 

Les principaux scientifiques ayant défini une échelle de température et les différentes substances chimiques employées soit comme points de références, soit pour leur variation de volume

Formules de conversion

On notera que contrairement aux degrés celsius, fahrenheit, réaumur, delisle ou  rømer, l’appellation « degré » kelvin a été abolie en 1967. Car, la température au sens de Kelvin est indépendante de toute mesure ou de toute substance. L’omission du mot « degré » et de son symbole associé tient à rappeler que cette température ne possède pas de point de référence arbitraire comme toutes les autres échelles de températures. Mais, constitue plutôt une unité absolue de mesure pouvant être manipulée dans les équations algébriques au même titre que l’énergie, la quantité de mouvement ou le moment cinétique par exemple.

Par définition, le kelvin est la fraction 1/273,16 de la température thermodynamique du point triple de l’eau. Ainsi, une variation de 1 K est équivalente à une variation de 1°C. L’échelle anglo-saxonne de Rankine (Ra), est quant-à-elle similaire à l’échelle de Kelvin. Mais, ajustée à l’échelle de Farenheit , ce qui met le point de congélation de la glace à 491,67°F. La conversion entre les différentes échelles se fait de la manière suivante:

K = (5/9)Ra = °C + 273,15 = (5/9)(°F -32) + 273,15 = (5/4)°Re + 273,15. 
Ra = (9/5)K = °F + 459,67 = (9/5)°C + 491,67 = (9/4)°Re + 491,67.