Calcul du spin du photon
Le calcul du spin d’un photon est simple si on assimile ce dernier à un anneau en rotation sur lui-même. Cette particule quantique n’a évidemment pas de masse au repos puisqu’elle se déplace à la vitesse de lumière c. Selon la relation de Planck-Einstein E = h·f, où f est la fréquence du photon et la relation d’Einstein E = m·c2, elle possède par contre une masse purement dynamique m = h·f/c2 :
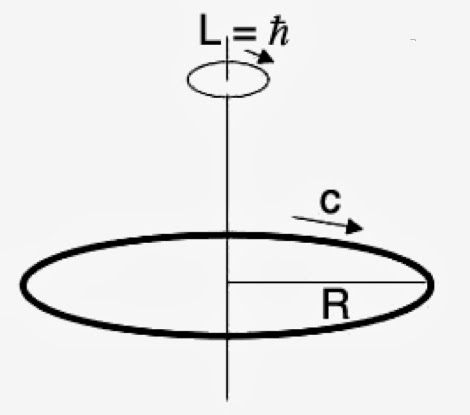
En accord avec la dualité onde-corpuscule de Louis de Broglie, pour que ce modèle soit viable, il faut que la longueur d’onde associée au photon λ soit égale à la circonférence de l’anneau 2π·R, soit :
\lambda = \frac{c}{f} = 2\pi R\Rightarrow R = \frac{c}{2\pi f}Or, le moment angulaire correspond, par définition, au produit de la quantité de mouvement p = E/c par la distance à l’axe de rotation R. Il vient donc :
\frac{E}{c}\cdot R = \frac{hf}{c}\cdot\frac{c}{2\pi f}\Rightarrow L = \frac{h}{2\pi} = \hbarÉtats de polarisation du photon
Le photon est donc bien une particule de spin entier égal à ħ. Selon les lois gouvernant le moment angulaire en physique quantique, le photon peut donc exister sous trois états de polarisation Sz = {-ħ, 0, +ħ}. L’état Sz = -ħ peut aisément être interprété comme un état de polarisation circulaire droite du photon :
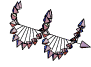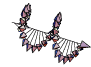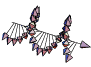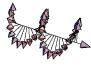
\hat S_z\left|-1\right> = -\hbar \left|-1\right>
De même, l’état Sz = +ħ peut s’interpréter comme un état de polarisation circulaire gauche du photon :
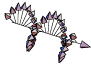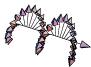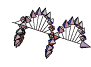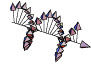
\hat S_z\left|+1\right> = +\hbar \left|+1\right>
Enfin, le photon ayant une masse nulle au repos, il ne peut jamais s’arrêter. Ceci fait que l’état |0> n’existe pas. Toutefois, il peut s’interpréter comme une combinaison linéaire des états droits et gauche, c’est-à-dire comme une onde plane :
\hat S_z\left[\left|+1\right> ± \left|-1\right>\right] = (\hbar-\hbar)\left[\left|+1\right> ± \left|-1\right>\right] = 0\left[\left|+1\right> ± \left|-1\right>\right]


Leave a Reply