Tenseur d’inertie

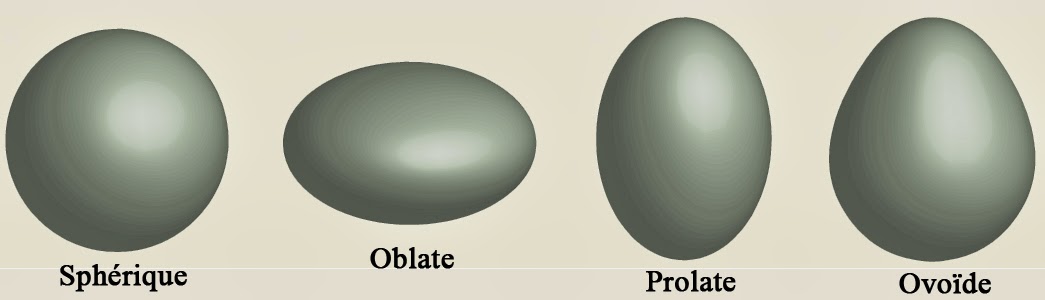
La molécule d’eau fait partie de la classe des toupies asymétriques. Il s’agit d’objets de forme ovoïde ou en forme de poire. Le tenseur d’inertie d’une toupie asymétrique possède trois valeurs principales. La plus petite valeur se note I_a tandis que la plus grande valeur se note I_c. La valeur intermédiaire se note quant à elle I_b. Une forme en soucoupe sera telle que I_a = I_b, la toupie étant qualifiée d’oblate. Une forme en cigare sera telle que I_b = I_c, la toupie étant alors qualifiée de prolate. Enfin, une toupie sphérique sera telle que I_a = I_b = I_c.

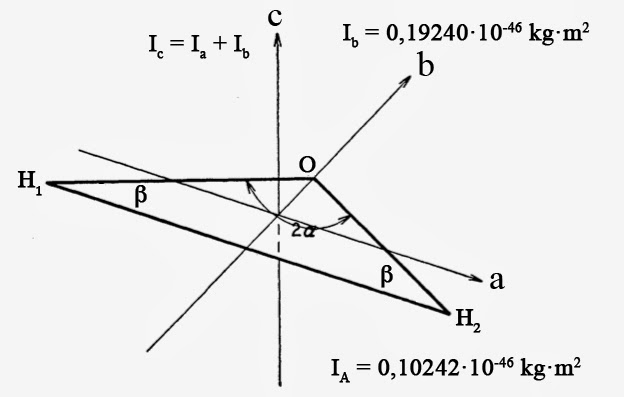
Pour des molécules planes, les axes principaux, a et b, sont dans le plan de la molécule. C’est le cas de la molécule d’eau H₂O. Le troisième axe, c, est lui perpendiculaire au plan de la molécule. On a alors la relation I_c = I_a + I_b.

Nombres quantiques

En physique classique, une toupie asymétrique tourne autour de l’axe de plus grande ou de moindre inertie. Cette rotation s’accompagne d’une précession ou nutation de période commensurable autour de la direction du moment angulaire total. D’autre part, il y a toujours conservation du moment angulaire et de l’énergie totale. Bien qu’un mouvement de rotation se fasse avec trois degrés de liberté, deux sont de nature périodique. En théorie quantique, on s’attend donc à ce que l’énergie soit fonction de trois nombres quantiques.

Le premier nombre noté J, a pour rôle de décrire le moment angulaire rotationnel total. Le deuxième nombre se note K_a. Il décrit la projection du moment angulaire le long de l’axe de plus faible moment d’inertie I_a. Il peut prendre toute valeur entière, sans dépasser la valeur J (K_a = 0, 1, 2,…, J). Enfin, le troisième nombre se note K_c. Il décrit la projection du moment angulaire le long de l’axe principal c de plus grand moment d’inertie I_c. Il peut prendre deux valeurs (K_c = J-K_a ou J – K_a + 1) si K_a ≠ 0.

Énergie de rotation

Par contre, si K_a = 0, il ne peut prendre qu’une seule valeur, K_c = J. On ne considère pas la projection selon l’axe principal I_b. En effet, gardons I_b constant pour une toupie asymétrique. Modifions sa forme de manière à ce que I_a = I_c = (I_a+I_c)/2. Dans ce cas, la toupie peut devenir indifféremment prolate, oblate ou sphérique. En revanche, gardons I_a constant. Déformons là de manière à ce que I_b = I_c = (I_b+I_c)/2. La toupie devient alors toujours oblate. Dans ce cas, son énergie ne dépend plus que des valeurs de J et de K_c :

A=\frac{\hbar^{2}}{2I_{a}};C=\frac{\hbar^{2}}{2I_{c}} \Rightarrow E(J,K_{c})=A\cdot J(J+1)-(A-C)\cdot K_{c}^{2}

Pour la molécule d’eau,  les constantes rotationnelles valent A = 27,1 cm^-1 et C = 9,5 cm^-1. Enfin, gardons I_c constant. Déformons la toupie de manière à ce que I_a = I_b = (I_a+I_b)/2. Cette dernière devient alors toujours prolate. Son énergie ne dépend maintenant plus que des valeurs de J et K_a :

E(J,K_a)=C\cdot J(J+1)+(A-C)\cdot K_a^2

Molécule d’eau

Pour une toupie de forme ovoïde comme l’eau, on peut introduire un facteur de déformation δ. Ce facteur est nul pour une toupie oblate et il vaut 1 pour une toupie prolate. Il est alors légitime de choisir les deux nombres “limites” K_a et K_c. Ces nombres expriment l’énergie de rotation d’un état quantique donné |J, K_a, K_c>. On peut alors montrer que :

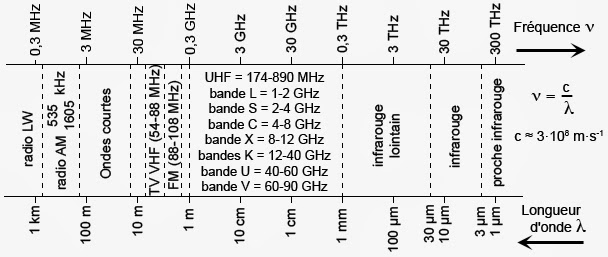
E(J,K_{a},K_{c})=\frac{A+C}{2}\cdot J(J+1)+\frac{A-C}{2}\cdot E\left (\delta =\frac{B-C}{A-C},K_{a},K_{c}\right )

Il existe des tables donnant les valeurs de la fonction E(δ, K_a, K_c). Les constantes rotationnelles de la molécule d’eau, fixent donc les écarts d’énergie existant entre les différents niveaux d’énergie. Le niveau fondamental de plus basse énergie est tel que J = 0. Il ne correspond qu’à un seul état noté |0,0,0>. Le premier état excité se caractérise par J = 1. Cet état possède un sous-état |1,0,1> à ∆E = 2C = 19 cm^-1. Le deuxième état |1,1,0> se trouve à ∆E = 2A = 52,1 cm^-1. Enfin, le troisième état |1,1,1> se trouve à ∆E = A+C = 36,6 cm^-1). Rappelons que 1 cm^-1 ≈ 30 GHz. Ces écarts d’énergies couvrent la bande de fréquence des microondes ainsi qu’une partie de l’infrarouge lointain :

États quantiques

Soit P₂ l’opération qui échange les labels ‘1’ et ‘2’ des deux atomes d’hydrogène de la molécule d’eau. Autrement dit, le proton en (x₁, y₁, z₁) passe en (x₂, y₂, z₂) et réciproquement. Ceci, sans bouger l’atome d’oxygène ni les électrons de la molécule. Cette opération doit  laisser l’énergie de la molécule invariante. On peut montrer que l’action de P₂ sur tout état |J, K_a, K_c> conduit à deux situations :

a) État rotationnel symétrique pour l’échange : P₂|J, K_a, K_c> = |J, K_a, K_c>. Pour cela, il faut que la somme (K_a+K_c) soit paire.
b) État rotationnel anti-symétrique pour l’échange : P₂|J, K_a, K_c> = -|J, K_a, K_c>. Pour cela, il faut que la somme (K_a+K_c) soit impaire.

Cette propriété de symétrie est importante en relation avec le principe d’exclusion de Pauli. Ce principe impose que l’état quantique total, incluant les électrons, les vibrations, les rotations et les spins nucléaires, soit toujours de caractère anti-symétrique lors de l’échange de deux fermions. Or, les protons se comportent comme deux fermions de spin nucléaire ½. Ces considérations impliquent donc l’existence de deux isomères de spin, appelés “ortho” et “para”.

Références

R.S. Mulliken, “Species classification and rotational energy patterns of non-linear triatomic molecules”, Phys. Rev., 59 (1941) 873-889.
G.W. king, R.M. Hainer, P.C. Cross, “The asymmetric rotor. I – Calculation and symmetry classification of energy levels”, Rev. Mod. Phys., 3 (1931) 280.