On appelle mode de vibration un type de mouvement au cours duquel le centre de gravité de la molécule reste immobile. De plus, le mode ne doit pas correspondre à l’un des 3 mouvements de rotation globale de la molécule autour de ses trois axes d’inertie principaux. Si le mouvement se fait en avec déplacement du centre de gravité, on parle de mouvement de translation. On rappelle qu’une molécule non linéaire constituée de N atomes possède 3 modes de rotation et 3 modes de translation. Cela laisse donc 3N-6 modes normaux de vibrations. Cette règle découle du fait qu’il faut trois 3 coordonnées (x, y, z) pour repérer la position d’un point dans l’espace. D’où un nombre total de degrés de liberté égal à 3×N.
Sur ces 3×N degrés de libertés, il faut en retirer trois qui correspondent à la translation du centre de masse selon chacun des axes x, y ou z. Puis, encore trois autres qui correspondent à la rotation autour du centre de masse selon les trois axes d’inertie (a, b, c) de la molécule. La molécule d’eau étant tri-atomique (N = 3) elle possède donc 3×N – 6 = 3×3 – 6 = 3 modes normaux de vibrations. Chaque mode présente une fréquence caractéristique f1, f2 et f3. Les symétries des vibrations associées à chacun de ces trois modes peuvent être déterminées au moyen de la théorie des groupes.
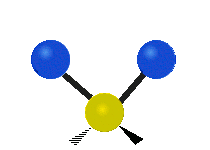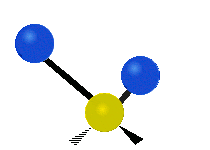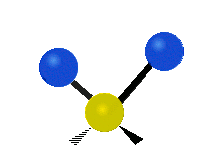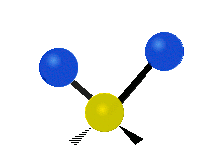
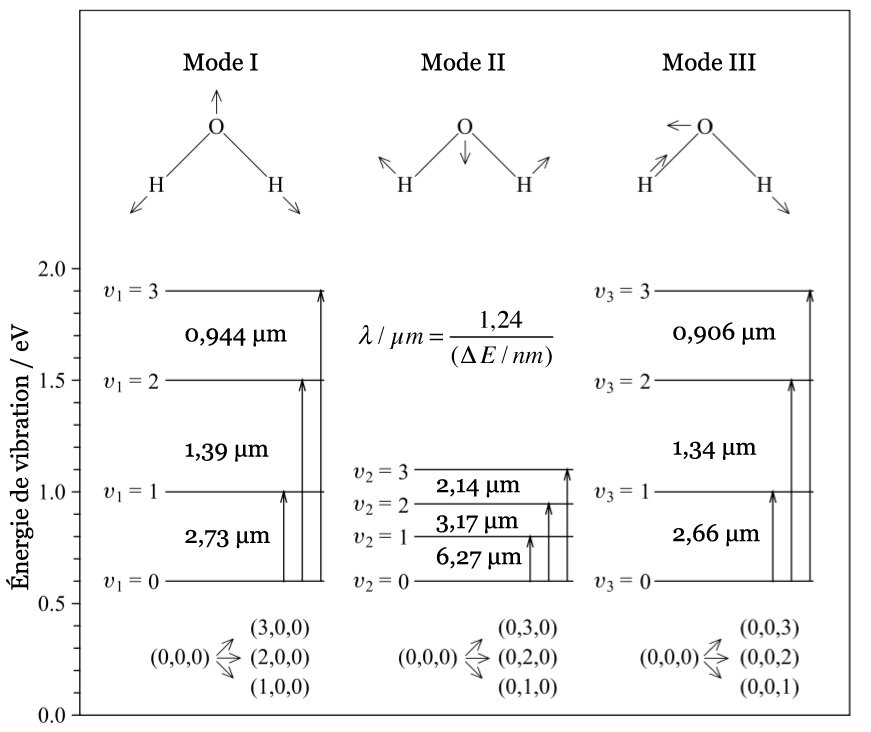
On trouve ainsi que le premier mode décrit un mouvement d’étirement totalement symétrique. Il appartient à la présentation irréductible a1 du groupe ponctuel C2v auquel appartient la molécule d’eau. Sa fréquence vaut f1 = 3657,053 cm-1. Au cours de ce mouvement, l’angle H-O-H reste constant tandis que les deux liaisons OH se raccourcissent ou s’allongent de manière symétrique.
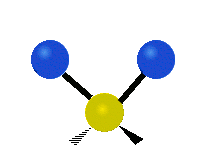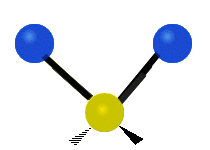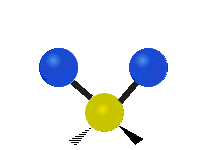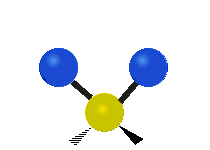
Le deuxième mode de vibration implique un mouvement de cisaillement. Il est lui aussi totalement symétrique avec le même symbole a1. Par contre, sa fréquence f2 = 1594,746 cm-1 est nettement plus basse. Au cours de ce mouvement, les distances O-H restent fixes tandis que l’angle H-O-H se ferme ou bien s’ouvre.
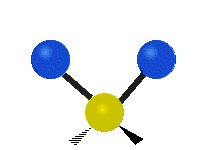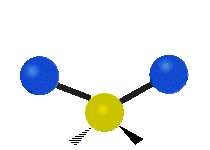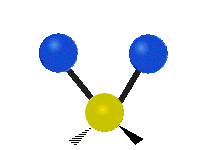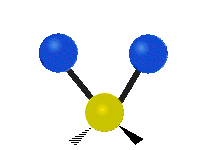
Enfin, le troisième mode de vibration implique un mouvement d’étirement asymétrique. Il appartient à la représentation irréductible b1 du groupe ponctuel C2v. Sa fréquence est très haute, valant f3 = 3755,929 cm-1. Au cours de ce mouvement, une distance O-H s’allonge tandis que l’autre se raccourcit en laissant l’angle H-O-H inchangé.
Tous les mouvements de vibration de la molécule d”eau peuvent ainsi être vus comme des combinaisons linéaires de ces trois modes normaux. Pour caractériser l’état quantique de l’eau du point de vue de ses vibrations moléculaires, il nous faudra donc 3 nombres quantiques associés à chacun de ces trois modes. On a l’habitude de représenter cela par le symbole de Dirac :
\mid v_{1},v_{2},v_{3}>Dans ces conditions, l’énergie de vibration de chaque état peut s’écrire :
E=EPZ+(h\cdot f _{1})\cdot v_{1}+(h\cdot f _{2})\cdot v_{2}+(h\cdot f _{3})\cdot v_{3}+E_{res}Ici, EPZ est l’énergie de point zéro de la molécule d’eau dans son état fondamental de vibration |0,0,0>. Elle s’exprime au premier ordre comme :
EPZ=\frac{h\cdot f _{1}+h\cdot f _{2}+h\cdot f _{3}}{2}L’énergie de point zéro est une énergie cinétique résiduelle de type purement quantique. Elle existe pour toute oscillation harmonique de fréquence f. Cette énergie est responsable du fait que la matière ne peut s’arrêter de vibrer même lorsque l’on se trouve au zéro absolu T = 0 K. Or, classiquement, tout mouvement devrait cesser lorsqu’on atteint le zéro absolu. La physique quantique invalide ce point de vue. Elle affirme que le repos n’existe pas dans la nature. Tout vibre, même au zéro absolu. L’énergie de point zéro se calcule moyennant la connaissance des fréquences associées à tous les modes normaux de vibration d’une molécule.
Comme on vient de le voir, l’eau se caractérise par trois modes normaux de vibration. La table suivante compare ainsi les énergies de point zéro pour cinq isotopologues ayant un atome d’oxygène présentant un excès de neutrons (9 ou 10) par rapport au nombre de protons (8). Ici A.N. désigne l’abondance naturelle de chaque isotopologue. Pour l’eau lourde D2O qui possède une abondance naturelle de seulement 0,00000268%, on trouve EPZ = 3319 cm-1, soit environ 40 kJ·mol-1. Le terme Eres représente quant à lui toutes les résonances possibles entre les 3 modes normaux :
E_{res}=X_{11}\cdot v_{1}^{2}+X_{22}\cdot v_{2}^{2}+X_{33}\cdot v_{3}^{2}+X_{12}\cdot v_{1}\cdot v_{2}+X_{13}\cdot v_{1}\cdot v_{3}+X_{23}\cdot v_{2}\cdot v_{3}Ici, les termes Xij sont des fonctions complexes des trois fréquences de base f1, f2 et f3. Les atomes d’hydrogène sont aussi des fermions. Il faut donc aussi se préoccuper du caractère symétrique ou anti-symétrique de chaque état vibrationnel vis-à-vis de l’échange des positions des deux protons. Cette opération de symétrie est représentée par le symbole P2. Or, les modes de nombre quantique v1 ou v2 décrivent des modes de nature totalement symétrique. On a donc, pour toute valeur de v1 ou de v2 :
P_{2}\mid v_{1},v_{2},v_{3}> =\mid v_{1},v_{2},v_{3}>En revanche, le mode associé au nombre quantique v3 est lui anti-symétrique pour l’échange des positions. Ceci signifie que les états où v3 est pair seront de type symétrique. Par contre, ceux où v3 est impair seront au contraire anti-symétriques :
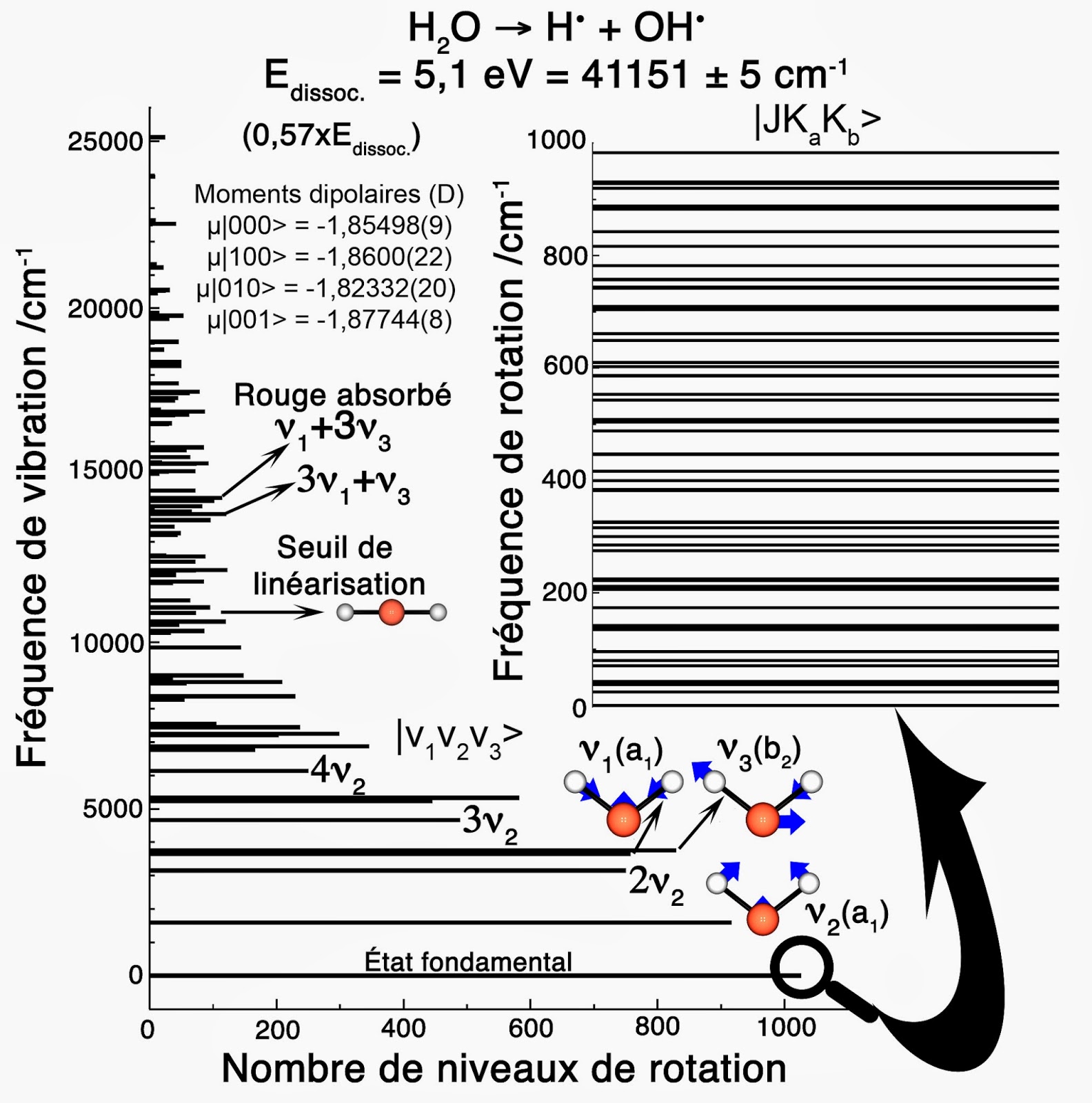
P_{2}\mid v_{1},v_{2},v_{3}> =(-1)^{v_3}\mid v_{1},v_{2},v_{3}>Cette propriété est importante en relation avec l’existence de deux isomères de spin “ortho” et “para” pour la molécule d’eau. La molécule d’eau isolée 16OH2 se caractérise ainsi par 12248 niveaux de vibration-rotation. Ils couvrent une gamme d’énergie de vibration (107 niveaux) allant jusqu’à 25 000 cm-1. La gamme d’énergie de rotation (1026 niveaux pour l’état fondamental |000>) va jusqu’à 21 000 cm-1. Pour mémoire, 1 eV = 1239,84 nm = 8065,5 cm-1. De même, l’énergie thermique kBT disponible à T = 300K correspond à une énergie de 208,5 cm-1 = 26 meV (kB = 0,695 cm-1·K-1). Enfin, la lumière visible couvre une gamme de nombre d’onde allant de 12 500 cm-1 (λ = 800 nm) à 25 000 cm-1 (λ = 400 nm).
Parmi les 107 niveaux de vibration, tous ceux qui ont une énergie supérieure à 12 500 cm-1 ne peuvent être atteints qu’en absorbant un photon de lumière visible. En particulier les deux harmoniques (ν1 + 3ν3) = 14924,84 cm-1 = 1,85 eV (λ = 670 nm) et (3ν1 + ν3) = 14727,09 cm-1 = 1,826 eV (λ = 679 nm) peuvent être excitées par des photons de couleur rouge. Ceci signifie que, sous une forte épaisseur, l’eau aura une couleur bleue. On notera également que le seuil de linéarisation par vibration-rotation de la molécule d’eau se situe à 11 105 ± 5 cm-1.
Références
B.T. Darlin, D.M. Dennison, “The water vapor molecule”, Phys. Rev., 57 (1940) 128-139.
Tennyson J. & al., «IUPAC critical evaluation of the rotational- vibrational spectra of water vapor. Part I Energy levels and transition wavenumbers for H217O, and H218O», J. Quant. Spectr. Rad. Transf., 110 (2009) 573-596.
Tennyson J. & al., «IUPAC critical evaluation of the rotational- vibrational spectra of water vapor. Part II Energy levels and transition wavenumbers for HD16O, HD17O and HD18O», J. Quant. Spectr. Rad. Transf., 111 (2010) 2160-2194.


Leave a Reply