Qui n’a pas vu une éponge absorber de l’eau liquide ? Mais, au fait pour quelle raison l’eau rentre-t-elle dans l’éponge ? Et, pour quelle raison il faut la presser pour faire ressortir l’eau absorbée ? Certaines personnes un peu pressées diront que c’est la différence d’hydratation qui explique le mouvement de l’eau entre deux corps. Or cela n’est pas exact. Plus précisément, ce n’est pas le taux d’hydratation qui permet de prédire le mouvement de l’eau. Mais, bien une grandeur appelée “activité de l’eau”. Pour comprendre cela, considérons un exemple concret.

Mélanger des poudres

Un marchand de soupe en poudre a voulu ajouter du poivre moulu à sa soupe pour la rendre plus épicée. Avant de faire le mélange, il veilla à choisir un poivre dont le taux d’hydratation était 3 pds%. Cette teneur en eau correspondait exactement à celle de la soupe. Pensant qu’il n’y avait aucun risque, il fit le mélange des deux poudres sèches. Il obtint alors dans son mélangeur une masse compacte impossible à manipuler. Il fut ainsi obligé de jeter non seulement tout le lot de soupe, mais aussi de passer un temps précieux à nettoyer sa machine afin de pouvoir l’utiliser à nouveau.

En fait, ce marchand avait tout simplement négligé de mesurer l’activité de l’eau de sa soupe et de son poivre. Il mesura donc l’activité de l’eau des deux ingrédients. Il constata ainsi que pour un même taux global d’hydratation (3 pds%) l’activité de l’eau dans la soupe en poudre était de 0,28. Celle du poivre sec était, elle, de 0,69, valeur très différente. Il était donc logique qu’après mélange intime des deux poudres, l’eau migre spontanément du poivre vers la soupe entraînant la formation de mottes compactes. Car, l’activité de l’eau dans le poivre était bien supérieure à l’activité de l’eau dans la soupe.

Diagramme de l’activité de l’eau

C’est précisément tout l’intérêt de cette notion d’activité que de savoir dans quel sens auront lieu les échanges de matière après mélange de deux substances. Cet exemple montre bien que connaître le taux d’hydratation ne renseigne en rien sur la disponibilité de l’eau. Seule l’activité de l’eau permet de savoir si l’eau sera facilement mobilisable, c’est-à-dire à haute activité. Ou bien, au contraire, si l’eau est difficilement mobilisable, c’est-à-dire de faible activité. Considérons la figure suivante. On constate qu’il est vrai que l’activité de l’eau augmente avec le taux d’humidité. Mais, cette variation est hautement non linéaire. L’activité de l’eau peut ainsi varier dans une grande gamme (0,1 à 0,6) pour un même taux d’humidité.

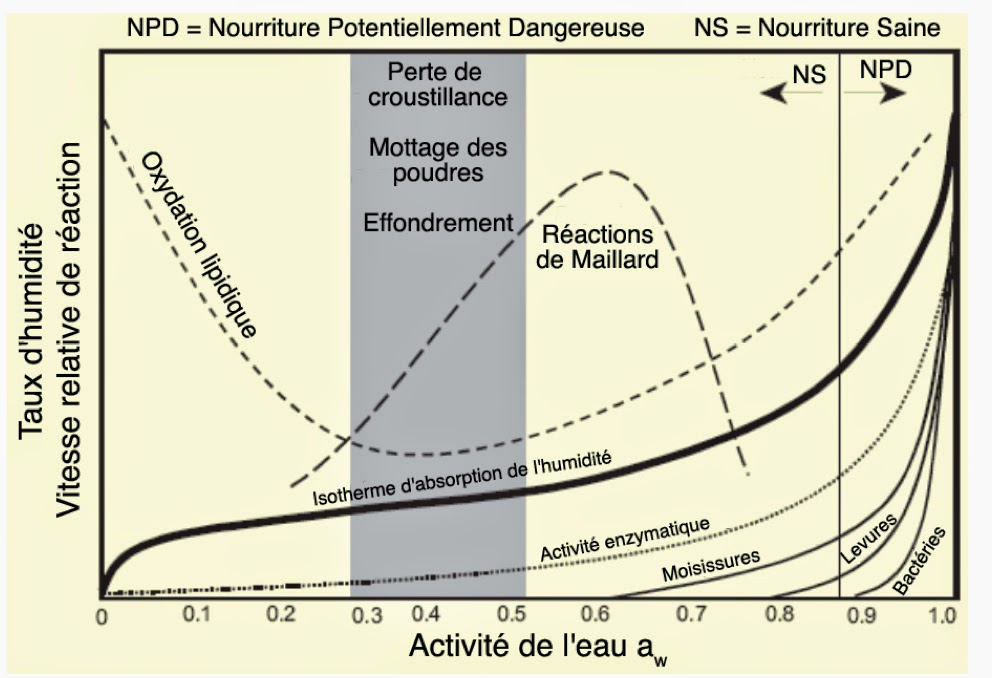
L’importance de ce concept d’activité de l’eau pour les processus biologique est bien illustré dans ce diagramme. On remarque ainsi, qu’aucune vie n’est possible lorsque a_W ≤ 0,6. À partir de cette valeur, seule la croissance de champignons est autorisée. Il faut pour cela que 0,6 ≤ a_W ≤ 0,8. Les levures ont quant à elles besoin d’une activité d’eau au moins égale à 0,8. La croissance bactérienne démarre pour sa part dès qu’a_W > 0,9. C’est d’ailleurs dans cette zone que l’activité enzymatique s’accroît de manière exponentielle.

Applications en cuisine

Le diagramme montre aussi qu’une nourriture sans conservateurs restera saine tant que l’on aura a_W ≤ 0,88. On y trouve aussi le domaine des réactions dites de “Maillard”. Ces réactions sont responsables du goût, de la couleur et de la texture lors de la cuisson des aliments. Elles se produisent avec une vitesse optimale lorsque a_W ≈ 0,6. L’oxydation lipidique se trouve pour sa part nettement défavorisée lorsque 0,3 ≤ a_W ≤ 0,5.

C’est dans cette même zone que les matériaux pulvérulents comme le sel auront tendance à motter. D’où l’emploi de grains de riz ,très secs, pour éviter la zone critique. C’est aussi dans cette zone qu’une croûte initialement croustillante deviendra molle et flasque. Ou bien alors qu’un tas de poudre ne s’effondrera plus sous l’action de la pesanteur aboutissant à la formation d’un cake. De manière plus chiffrée, la table suivante donne l’activité de l’eau et le taux d’hydratation pour quelques aliments communs.

Alimentation

Utilisés conjointement, cette figure et cette table permettent tout de suite de comprendre ce que l’on appelle une denrée périssable qui se caractérise par a_W ≥ 0,87. On voit aussi qu’il existe des denrées non périssables pouvant être gardées très longtemps en l’absence d’eau à condition que a_W < 0,6. Par conséquent, il est maintenant accepté que l’activité de l’eau est très intimement liée aux propriétés physiques, chimiques et biologiques des aliments. Et, ce bien plus que le taux d’hydratation. De fait, il peut y avoir des changements spécifiques de couleur, d’arômes, de goût, de texture, de stabilité et d’acceptabilité d’aliments crus ou cuisinés. Ceux-ci sont toujours associés à des domaines assez étroits d’activité de l’eau.

Origine physique

Nous avons maintenant compris l’importance de l’activité de l’eau. Il reste donc à comprendre quel est le réel sens physique de cette notion. Ceci de manière à savoir comment l’évaluer et la mesurer. Pour cela, considérons tout d’abord de l’eau pure à l’état liquide se trouvant en contact avec l’air. Dans le liquide, il existe des forces intermoléculaires qui empêchent les molécules d’eau présentes à la surface de s’échapper dans la phase gazeuse. Toutefois, les molécules d’eau sont soumises à l’agitation thermique. Il peut donc arriver qu’une molécule de surface possède une énergie cinétique suffisante pour vaincre l’énergie potentielle associée aux différentes forces intermoléculaires de la phase condensée.

A l’inverse, une molécule d’eau gazeuse, proche de la surface, peut se voir happée par cette dernière. Cela se produit si son énergie cinétique devient inférieure à l’énergie potentielle de condensation. Lorsque l’équilibre thermodynamique est atteint, le nombre de molécules d’eau qui passent vers la phase gaz est exactement égal au nombre de molécules d’eau qui se collent à la surface. Dans ces conditions, il existe une pression de vapeur saturante P_S du liquide dans la phase gazeuse. Cette pression de vapeur saturante dépend uniquement de la température.

Notion de pression de vapeur

Soit P_V la pression de vapeur d’un liquide et P la pression extérieure P. Il y aura ébullition dès que P_V < P < P_S, évaporation si P_V < P_S < P et condensation lorsque P < P_V < P_S. Le point d’ébullition T_eb est la température pour laquelle  P = P_S. Une situation d’équilibre se caractérisera quant-à-elle par P_V = P_S. Pour un équilibre solide ⇄ gaz ou liquide ⇄ gaz, la relation de Clausius-Clapeyron permet d’exprimer la variation de la pression de vapeur saturante avec la température. Cette dernière est fonction de la chaleur latente de vaporisation L_V et de la constante des gaz parfaits R :

dP = \frac{{{L_v}}}{V} \cdot \frac{{dT}}{T} \Rightarrow \ln \frac{{{P_S}}}{{P^\circ }} = \frac{{{L_v}}}{R}\left( {\frac{1}{{{T_{eb}}}} - \frac{1}{T}} \right)

Par exemple, pour l’eau on a L_V(25°C) = 41,8 kJ.mol^-1, soit P_S ≈ 3,2 kPa pour P° = 101,325 kPa. Que se passe-t-il maintenant si une partie des molécules d’eau présentes en surface sont remplacées par une substance de nature chimique différente ? On s’attend, pour une même température T, à ce que la pression de vapeur P_V de l’eau soit plus faible. En effet, une partie de la surface occupée par le soluté n’est dorénavant plus accessible à l’eau. Le rapport entre la pression de vapeur d’eau P_V dans toute substance hydratée et la pression de vapeur saturante de l’eau pure P_S à la même température définit ce que l’on appelle « activité de l’eau » :

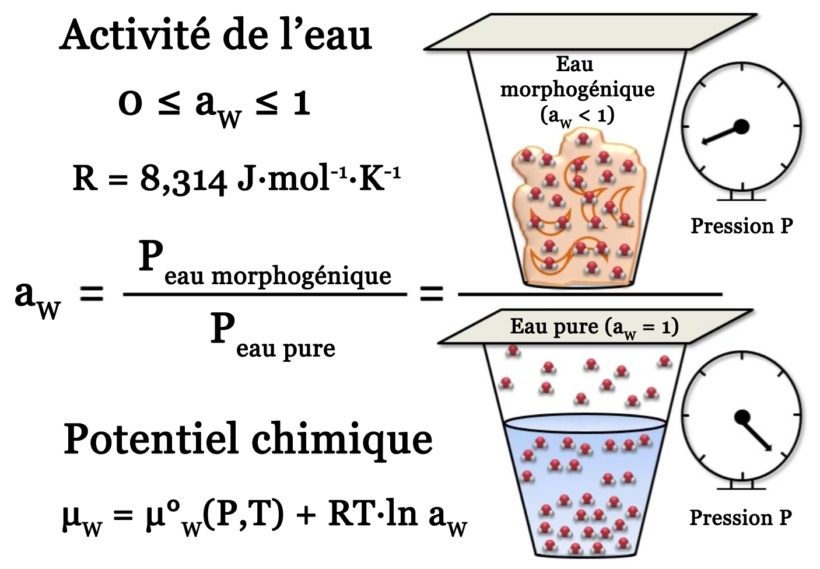
0 ≤ a_W = P_V/P_S ≤ 1

En conséquence, ce paramètre possède un sens physique clair et non ambigu. Il est de plus aisément mesurable au moyen d’appareils appelés « hygromètres » [3].

Relation de Gibbs-Duhem

Rappelons que les processus vitaux ne se placent pas dans le cadre de l’approximation des solutions extrêmement diluées. Une cellule contenant en moyenne 70 pds% d’eau, l’eau constitue bien la phase majoritaire (solvant). Mais, avec 30 pds% de soluté, parler de milieu extrêmement dilué n’a aucun sens.  Il est donc complètement irréaliste d’utiliser la loi de van’t Hoff pour quantifier la notion d’activité de l’eau. Un traitement utilisant la notion de potentiel chimique s’avère dans ces conditions nécessaire.

Soit donc P la pression, T la température et μ_W = μ°_W + RT·ln a_W le potentiel chimique de l’eau. On l’exprime ici via son activité 0 < a_W ≤ 1. Ici, R est la constante des gaz parfaits égale à 8,314 J·mo^l-1·K^-1. Enfin, μ°_W est le potentiel chimique de l’eau lorsque a_W atteint sa valeur maximale 1. Considérons maintenant es 4 variables thermodynamiques (p, T, μ_W, a_W). On peut écrire en toute généralité l’identité suivante :

{\left( {\frac{{\partial p}}{{\partial {a_W}}}} \right)_{T,{\mu _W}}} \cdot {\left( {\frac{{\partial {a_W}}}{{\partial {\mu _W}}}} \right)_{T,p}} \cdot {\left( {\frac{{\partial {\mu _W}}}{{\partial p}}} \right)_{T,{a_W}}} =  - 1 \Rightarrow {\left( {\frac{{\partial p}}{{\partial {a_W}}}} \right)_{T,{\mu _W}}} =  - {\left( {\frac{{\partial p}}{{\partial {\mu _W}}}} \right)_{T,{a_W}}} \cdot {\left( {\frac{{\partial {\mu _W}}}{{\partial {a_W}}}} \right)_{T,p}}

Remarquons que la première dérivée à droite de cette expression correspond à l’inverse du volume partiel V_m de l’eau. En effet, appliquons le premier principe à l’eau pure (a_W = 1) en fonction du nombre de moles d’eau N_W :

dG = d(N_W·μ_W) = -S·dT + V·dP + μ_W·dN_W, ⇒ N_W·dμ_W = -S·dT + V·dP

Ici, V le volume disponible et S l’entropie associée (équation de Gibbs-Duhem). Il s’ensuit que pour tout processus isotherme (dT = 0) on a dμ_W = V_m·dP. On retrouve donc V_m = V/N_W = (∂μ_W/∂P)_T qui est le volume molaire de l’eau à la température considérée. Compte tenu de la définition du potentiel chimique de l’eau, il vient :

{\left( {\frac{{\partial p}}{{\partial {a_W}}}} \right)_{T,{\mu _W}}} =  - \frac{{RT}}{{{V_m}\cdot{a_W}}} \Rightarrow \int_p^{p + \Pi } {dp}  =  - \frac{{RT}}{{{V_m}}}\int_1^{{a_W}} {\frac{{d{a_W}}}{{{a_W}}}}  \Rightarrow \Pi  \cdot {V_m} =  - RT \cdot \ln {a_W}

Pression d’imbibition

On voit donc qu’en toute généralité, toute variation de l’activité a_W de l’eau se traduit par l’apparition d’une pression mécanique Π. Cette pression est évidemment nulle pour l’eau pure (a_W = 1). Dès que l’eau entre en contact avec un soluté (électrolyte) ou une matière solide (protéine) son activité ne peut que diminuer. Ceci créé alors une pression d’autant plus forte que l’activité est plus basse. En toute rigueur, il faudrait considérer dans cette relation le volume molaire partiel de l’eau. C’est-à-dire le volume occupé par une mole d’eau compte tenu de toutes les interactions intermoléculaires auxquelles participe la molécule d’eau dans le milieu considéré.

Néanmoins, on peut avoir un ordre de grandeur des pressions mises en jeu, en prenant la valeur V_m ≈ 18 cm³·mol^-1 (eau pure). Ceci nous donne la constante piézoscopique de l’eau, R/V_m ≈ 0,46 MPa·K^-1 et avec 1 atm = 101,325 kPa. Ainsi, l’eau de mer qui possède une activité de l’eau a_W = 0,98 développe une pression Π ≈ 2,8 MPa ≈ 28 atm. Cette pression peut monter jusqu’à 400 atm pour une eau saturée en chlorure de sodium (a_W = 0,75). Pour une monocouche de molécule d’eau adsorbée à la surface d’un colloïde hydrophile on peut avoir 0,2 ≤ a_W ≤ 0,4. Ceci correspond à des pressions dans la gamme 1000-2000 atm. Avec de tels chiffres, rien ne résiste à la poussée d’une graine arrosée d’eau ou d’un bout de bois sec que l’on hydrate brusquement.

Références

[1] Rockland L.B. & Nishi S. (1980), «Influence of water activity on food products quality and stability», Food Technology, 34, 42-51.

[2] Rockland L.B. & Beuchat L.R. (1987), in «Water activity: theory and application to food», Marcel Dekker, New-York, Introduction.

[3] Wiederhold P.R. (1997), «Water vapor measurements: methods and instrumentation», Marcel Dekker, New-York.