Particules et champs

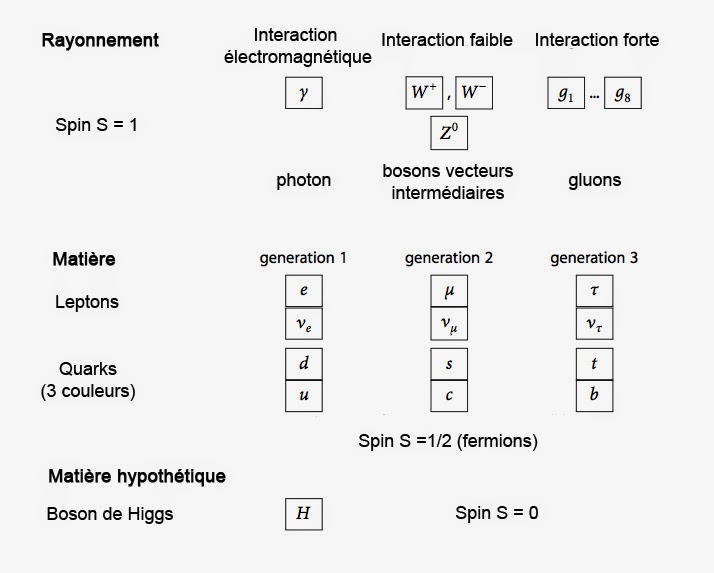
La physique quantique des champs voit le monde comme un jeu de particules élémentaires. On y trouve ainsi des “fermions” de spin demi-entier interagissant au moyen d’autres particules appelées bosons (spin entier). Ces particules qui peuvent être « virtuelles » représentent des excitations de champs quantiques. D’où aussi un aspect ondulatoire associé aux excitations collectives de ces champs. Parmi, l’ensemble de toutes les particules élémentaires de la physique, l’électron, le proton et le neutron se combinent en grand nombre pour donner naissance à ce que l’on appelle la matière. Cette matière forme le monde macroscopique de la vie de tous les jours.

Dans ce monde quantique, les photons sont des bosons de spin 1. Ils sont très nombreux et forment le spectre des ondes électromagnétiques. En théorie quantique des champs, on ne parle plus d’onde ou de particules, mais plutôt de champs quantiques. Rappelons que les entités dynamiques de la physique classique sont soit des particules, soit des champs. Toute particule possède une position définie à un moment donné. L’équation de Newton permet de prédire comment cette position bien définie va évoluer dans le temps sous l’action de différentes forces. Ceci donne alors naissance à la notion de trajectoire. 

Champs classiques

Par contraste, un champ classique 𝜙(x,y,z,t) est une quantité qui varie de manière continue dans un espace tridimensionnel. Cet espace est muni dans chacune des trois directions indépendantes de la topologie usuelle de l’ensemble des nombres réels. Les champs ont eux aussi une dynamique gouvernée par des équations différentielles. Par exemple, via les équations de Maxwell dans le cas du champ électromagnétique. La physique classique des champs cherche donc à prévoir comment les champs varient dans le temps et l’espace. L’espace étant ici une variété continue, il existe une triple infinité de positions spatiales. Ceci implique donc un nombre de degrés de libertés infinis pour le champ.

Un système physique classique le plus général contient donc des particules et des champs. Dans ces conditions comment quantifie-t-on un champ ? Rappelons que pour une particule, les observables classiques sont la position et la quantité de mouvement. Les autres quantités comme le moment cinétique angulaire ou l’énergie sont des concepts dérivés. Elles s’expriment au moyen de ce seul couple de variables dynamiques. Or, la quantification d’une particule se fait en remplaçant les observables positions et quantité de mouvement par des opérateurs. On représente de tels opérateurs par une lettre possédant un chapeau. Ils agissent dans un espace mathématique abstrait appelé « espace de Hilbert ».

Première quantification

Dans la représentation de Schrödinger de la mécanique quantique, c’est l’opérateur position qui joue un rôle de premier plan. Ici, des opérateurs qui ne dépendent pas du temps agissent sur une fonction d’onde ψ(x, y, z, t). Cette fonction obéit à une équation différentielle du premier ordre par rapport au temps. Par contre, cette équation est du deuxième ordre par rapport à l’espace (équation de Schrödinger). Les autres observables  comme le moment cinétique angulaire ou l’énergie deviennent elles aussi des opérateurs.

Toute la mécanique quantique des particules découle de l’existence de relations de commutations ou de non-commutation entre les différents opérateurs. Ces relations de commutation fondamentales sont en fait au cœur de la quantification d’un système de particules matérielles non relativistes. Le premier champ à être quantifié fut le champ électromagnétique, car il existait déjà en physique classique. La théorie quantique du champ électromagnétique remonte au milieu des années 1920 durant la formalisation de la mécanique quantique.

Électrodynamique quantique

L’électrodynamique quantique fut conçue dès le départ pour rendre compte de la création et de la destruction des photons. Le photon émerge naturellement comme le quantum associé au champ électromagnétique dans le cadre de cette théorie. Par la suite, les physiciens durent inventer d’autres champs, parfaitement inconnus en physique classique. Ces champs doivent, eux aussi, être quantifiés pour expliquer l’existence d’autres particules que le photon. Il existe, par exemple, un champ qui peut créer ou détruire des électrons. Les théories anciennes avaient pour habitude d’utiliser d’autres champs pour expliquer l’existence des protons, des neutrons ou des pions.

De nos jours, on a atteint un niveau de compréhension plus fondamental. Ce niveau considère des quanta appelés quarks et gluons. Toutefois, ces quanta peuvent, eux aussi, être créés et détruits à volonté. La théorie quantique des champs définit une densité d’énergie qui jouera le rôle d’Hamiltonien, opérateur associé à l’observable énergie. On considère ainsi que chaque point (x, y, z) de l’espace est maintenant un champ (x, y, z, t). Par dérivation par rapport au temps, on obtient un moment associé π(x, y, z, t). Il suffit alors d’introduire un ensemble de relations de commutation. Ces relations font intervenir des intégrales impliquant un volume infiniment petit centré sur le point spatial considéré.

Création et annihilation

La recherche des valeurs propres associées aux nouveaux opérateurs conduit alors à un résultat remarquable. En effet, il émerge spontanément du champ quantique une particule douée d’une masse m et d’une quantité de mouvement p. Ces deux variables sont telles que le carré de l’énergie E s’exprime comme E² = p²·c² + m²·c⁴. Un autre résultat intéressant est qu’il existe aussi un état unique de masse nulle et de quantité de mouvement nulle. Cet état décrit un état de vacuité, appelé vide quantique. En fait par combinaisons linéaires, il existe aussi des états pour n’importe quel nombre de particules. Chaque particule possède une énergie et une quantité de mouvement. L’énergie totale étant la somme des contributions de chaque particule individuelle.

Notons qu’en physique quantique des champs les quanta peuvent apparaître ou disparaître à n’importe quel moment. Au départ, il n’y a aucune particule. Car celles-ci émergent comme les excitations ou les quanta d’un champ quantique donné. L’espace de Hilbert n’existe donc plus dans ce type de physique et se trouve remplacé par un « espace de Fock ». Dans ce nouvel espace, on dénombre, en chaque point de l’espace-temps, le nombre de quanta présents. De plus, les états à plusieurs particules dérivent tous d’un même champ quantique. Toutes les particules apparaissent donc avec nécessairement la même masse et la même charge. Autrement dit, ces particules sont parfaitement indiscernables.

Phase quantique

Ceci est en très net contraste avec la physique quantique corpusculaire. Car ici le nombre total de particules était une donnée initiale qui ne pouvait varier dans le temps. Le fait que les particules élémentaires soient indiscernables était une évidence découlant de l’expérience et non de la théorie. En physique quantique des champs, le nombre de particules devient donc une observable. Il existe donc un opérateur associé qui possède un spectre de valeurs et de vecteurs propres. D’où aussi un principe d’indétermination impliquant nombre de quanta et phase quantique.  

Rappelons qu’en physique quantique il est possible d’associer à tout état d’énergie E une fréquence f  = E/h. Chaque état possède aussi une phase quantique φ = 2πE·t/h = 2πf·t. Maintenant, l’énergie totale E devient une fonction du nombre total de quanta selon E = N·hf. Toute fluctuation d’énergie ∆E dure un laps de temps ∆t = ∆φ/2πf. Ceci correspond donc à une fluctuation du nombre de quanta ∆N = ∆E/hf.  Soit maintenant la relation d’incertitude liant temps et énergie ∆E·∆t ≥ ℏ/2. Il en découle donc ∆N·hf· ∆φ/2πf ≥ ℏ/2, soit après simplification : ∆N·∆φ ≥ 1/2.

La physique quantique des champs permet aussi de justifier la loi de conservation de la charge électrique. Car, selon le théorème de Noether, une telle conservation provient de la relativité de l’origine pour mesurer la phase quantique. Ce principe de relativité est lui-même associé à l’opération de symétrie qui change l’angle de phase d’une quantité infinitésimale dφ. Ceci a pour conséquence que toute information codée au niveau d’une phase quantique ne sera pas mesurable physiquement. Seuls les effets liés aux différences de phase pourront être observés.