Champ magnétique et lumière

Michael Faraday échoua à mettre en évidence l’effet d’un champ magnétique sur la fréquence de la lumière. Ceci n’empêcha pas le physicien hollandais Peter Zeeman de reprendre ses expériences. En 1893, il utilisa une flamme de sodium. Il constata lui aussi que rien ne se passait. A l’instar de Faraday, il suspectait un lien étroit entre optique et magnétisme. Cela valait donc le coup de persévérer. Aussi, en août 1896 dans son laboratoire de l’université de Leyde, il répéta l’expérience. Il utilisa pour cela un électroaimant parcouru par un courant de 27 ampères. Une flamme de bec Bunsen alimentée par de petites quantités de sodium permettait de générer la lumière. Ce dernier provenait d’un morceau d’amiante imprégné avec du sel de cuisine. Zeeman plaça le morceau d’amiante entre les pôles de l’électroaimant.

Or, chaque fois qu’il faisait passer le courant, les deux raies D se trouvaient significativement élargies. Il répéta plusieurs fois l’expérience dans des conditions différentes. Sûr du phénomène, il publia ses résultats dès 1896 dans un journal hollandais obscur. Heureusement, l’article fut traduit en anglais [1]. Zeeman y concluait à la modification de la période de la lumière du sodium par la présence d’un champ magnétique. Dix ans auparavant Heinrich Hertz avait démontré le rôle fondamental joué par les champs électrique et magnétique dans la propagation de la lumière. Zeeman venait, lui, d’établir de manière quasi certaine leur rôle non moins fondamental dans la production de cette même lumière.

Le calcul de Lorentz

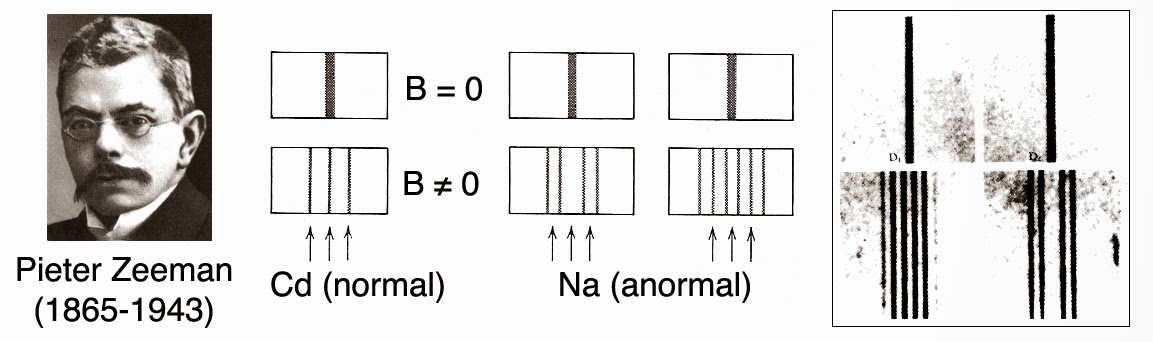
En 1897, Zeeman employa un puissant aimant de 3,2 teslas. Il arriva ainsi à résoudre la raie rouge du cadmium à 6438,47 Å en deux raies (doublets) pour l’observation longitudinale. Toutefois, il obtenait trois raies (triplets) pour l’observation transversale. Zeeman était un expérimentateur et non un théoricien. Il consulta donc son collègue hollandais Hendrik Lorentz. Celui-ci compris tout de suite comment interpréter les résultats de Zeeman. Il suffisait pour cela de considérer l’électron comme une particule liée de manière élastique au noyau. Or, il se trouve que la force de Lorentz est toujours perpendiculaire au plan défini par la vitesse de déplacement et la direction du champ magnétique.

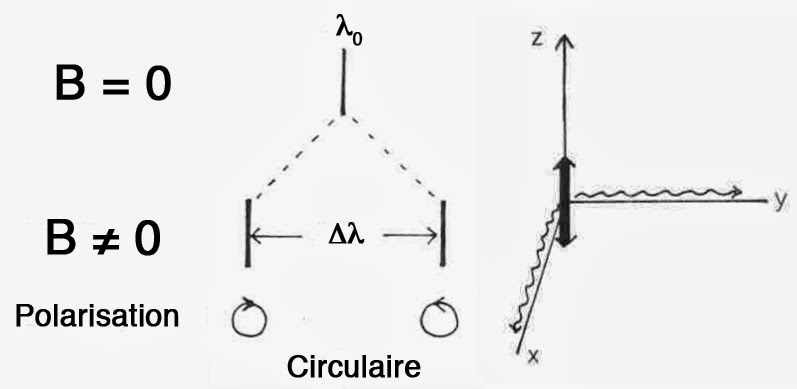
Lorentz décomposa alors le mouvement de l’électron en une vibration linéaire dans la direction z du champ magnétique appliqué. Une telle vibration correspond en fait à deux mouvements circulaires de directions opposées exécutés dans le plan perpendiculaire (x, y) à la direction du champ. Avec ce modèle, Lorentz considéra la lumière vue de manière longitudinale. C’est-à-dire dans la direction des lignes de force du champ. Il prédit une polarisation circulairement de cette lumière. Car, la lumière provient alors d’électrons se déplaçant selon des orbites circulaires. Selon ce modèle, les électrons vibrant dans la direction du champ ne pouvaient émettre aucune lumière. On s’attend dans ce cas à observer deux raies.

Restait à calculer l’écart en fréquence entre ces deux raies. Lorentz fit appel à la physique classique. Il considéra qu’il existait une force mécanique centrifuge m·v²/. Pour la contre-balancer, invoqua une force de rappel k·r et la force de Lorentz e·v·B. Ceci permettait d’évaluer les fréquences des deux mouvements circulaires :

\begin{gathered} k=4\pi ^{2}\cdot m\cdot \nu _{0}^{2} \\ v=2\pi r\cdot \nu \end{gathered}\Rightarrow\frac{m\cdot v^{2}}{r}=k\cdot r+e\cdot v\cdot B\Rightarrow \nu \approx \nu _{0}\pm \frac{e\cdot B}{4\pi m}

Électrons et lumière

Lorentz considéra également le cas d’une lumière observée de manière transversale, Son modèle prédisait l’observation d’une fréquence non affectée par le champ avec une polarisation linéaire. Car, la lumière provenait d’une oscillation des électrons dans la direction du champ (x ou y). Pour le mouvement circulaire dans le plan (x, y), la composante y pouvait émettre une lumière selon la direction x. En revanche, la composante x émettait selon la lumière selon la direction y. Ici, le champ magnétique accélère l’une des composantes et ralentit l’autre. On s’attend donc à observer 3 raies, toutes de polarisation linéaire. Lorentz publia son interprétation en 1897. Il suggéra aussi la mesure du rapport charge/masse de l’électron via l’action d’un champ magnétique sur les fréquences d’émission des atomes.

Zeeman confirma aussitôt cette prédiction de manière expérimentale. La même année, J. J. Thomson mesura ce rapport charge sur masse au moyen de rayons cathodiques et de rayons β. Il constata un bon accord avec les mesures de Zeeman sur les atomes. Il devenait ainsi quasiment certain que l’électron était un constituant des atomes. De même, il apparaissait comme le principal responsable de l’émission de lumière par ces mêmes atomes. De plus, il y avait la polarisation circulaire de la composante de courte longueur d’onde. Cette composante se caractérisait par le même sens de rotation que le courant dans un électroaimant. On prouvait donc que l’électron (ou électricité résineuse) avait une charge électrique négative.

Un effet “anormal”

Tout semblait donc aller pour le mieux. Sauf qu’en cette fin d’année 1897 le physicien irlandais Thomas Preston (1860-1900) utilisa la raie bleue à 4800 Å du cadmium. Il constata alors l’apparition de quadruplets (4 raies) au lieu des triplets attendus. Il montra aussi que la raie D₁ du sodium donnait également 4 raies sous la forme de deux doublets. La raie D₂ donnait pour sa part naissance à six raies (sextuplet). Or, la théorie de Lorentz ne prévoyait que 2 ou 3 raies. Tout ceci était parfaitement anormal. On baptisa ainsi ce comportement étrange : “effet Zeeman anormal”.

Le problème de ces nombreux multiplets spectraux devint l’un des problèmes central de physique quantique. De fait, il allait devenir pendant près de 30 ans un casse-tête insurmontable pour bon nombre des meilleurs physiciens de l’époque. Sa résolution satisfaisante se fera par l’introduction de la notion de “spin”.

Référence

[1] « On the influence of magnetism on the nature of light emitted by a substance », Phil. Mag. (1897), 43: 226-239.