Réactions d’oxydo-réduction

La notion de nombre d’oxydation est fondamentale pour l’équilibrage des réactions impliquant des transferts d’électrons. On parle dans ces conditions de réactions d’oxydo-réduction. On rappelle ici une méthode simple et fiable pour accéder à ces nombres d’oxydation. Premièrement, il faut dessiner une structure de Lewis du composé ou de l’ion étudié. Deuxièmement, il faut prendre soin de bien montrer toutes les paires d’électrons liantes ou non liantes. Quand des formes résonnantes existent, une seule structure suffit.

Ensuite, pour chaque paire liante A-B, on cherche l’atome le plus électronégatif. Si c’est l’atome B, on affecte alors les deux électrons de la liaison à B. Si A et B possèdent la même électronégativité, on donne un électron à A et l’autre électron à B. Chaque atome garde en propre sa ou ses paires non liantes. On procède ainsi pour chaque liaison chimique. Ceci fait, on soustrait le nombre d’électrons présent autour de chaque atome du nombre d’électrons de valence de l’atome libre. La différence est le nombre d’oxydation cherché.

Notion d’électronégativité

Pour mémoire l’électronégativité EN est un nombre compris entre 1 et 4 que l’on obtient en utilisant les règles suivantes :

Élément 1s : H = 2,1

Alcalins (2s, 3s, 4s, 5s, 6s) : Li, Na, K, Rb, Cs = 1,0

Éléments (2s, 2p) : ajouter 0,5 en partant de Li. Soit : Be = 1,5 B = 2,0 C = 2,5 N = 3,0 O = 3,5 F = 4,0

Éléments (3s, 3p) : ajouter 0,3 à partir de Na. Soit :Mg = 1,3 Al = 1,6 Si = 1,9 P = 2,2 S = 2,5 Cl = 2,8

Éléments (4s, 4p) : ajouter 0,25 à partir de K. Soit : Ca = 1,25 Ga = 1,5 Ge = 1,75 As = 2,0 Se = 2,25 Br = 2,5

Éléments (5-6s, 5-6p) : ajouter 0,2 à partir de (Rb,Cs). Soit (Sr,Ba) = 1,2 (In,Tl) = 1,4 (Sn,Pb) = 1,6 (Sb,Bi) = 1,8 (Te,Po) = 2,0 (I,At) = 2,2

Éléments d = 1,2 à 1,9

Éléments f = 1,2

Nitroguanidine

La nitroguanidine est une molécule qui possède plusieurs atomes d’azote présentant des nombres d’oxydation différents :

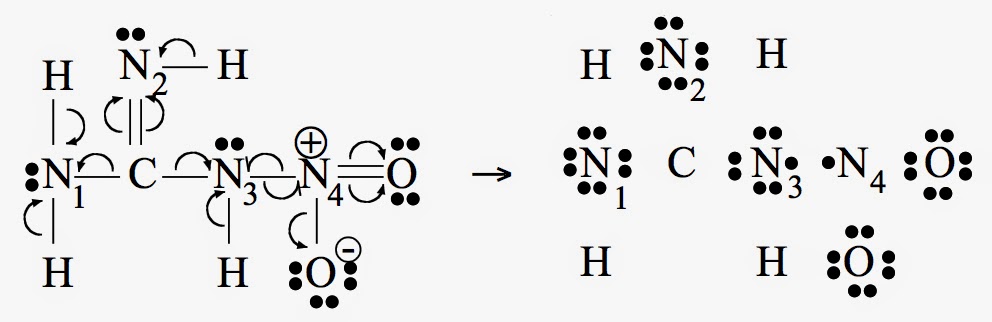
Pour les liaisons N-H, c’est l’azote qui prend les 2 électrons puisque EN(N) = 3,0 > EN(H) = 2,1. Pour les liaisons C-N, c’est l’azote qui prend encore les 2 électrons puisque EN(N) = 3,0 > EN(C) = 2,5. En revanche, pour les liaisons N-O, c’est l’oxygène qui prend les 2 électrons puisque EN(O) = 3,5 > EN(N) = 3,0. Enfin, pour la liaison N-N, chaque atome d’azote prend 1 électron, car il y a ici égalité des électronégativités.

Ayant distribué les électrons (formule de droite), il ne reste plus qu’à compter le nombre d’électrons autour de chaque atome. On utilise pour cela le fait que l’atome d’hydrogène non lié possède 1 électron de valence. De même, le carbone en possède 4, l’azote 5 et l’oxygène 6. Par convention, on utilise des chiffres romains :
Ox(H) = 1 – 0 = +I
Ox(C) = 4 – 0 = +IV
Ox(O) = 6 – 8 = -II
Ox(N1, N2) = 5 – 8 = -III
Ox(N3) = 5 – 7 = -II
Ox(N4) = 5 – 1 = +IV.

On voit donc que l’azote existe sous trois états d’oxydation différents dans cette molécule.

Espèces cristallines

La méthode est générale pour toute espèce moléculaire où l’on peut écrire une structure de Lewis. Pour les espèces cristallines existant à l’état solide, on procède différemment. On suppose ici que les atomes (F, Cl, Br, I) possèdent le degré d’oxydation -I. De même, on suppose que les atomes (LI, Na, K, Rb, Cs) possèdent le degré d’oxydation de +I.  Les atomes (O, S et Se) possèdent le degré d’oxydation -II s’ils ne sont pas liés à eux-mêmes. Dans le cas contraire, ils possèdent le degré d’oxydation -I.

Les atomes (Be, Mg, Ca, Sr et Ba) ont pour leur part un degré d’oxydation de +II à l’état solide. Enfin, l’atome d’hydrogène, possède un degré d’oxydation de +I sauf s’il n’est pas lié à un métal. Dans le cas contraire, son degré d’oxydation est -I. On joue finalement sur le fait que la somme de tous les degrés d’oxydation du solide doit toujours être nulle. Ceci permet de déduire le nombre d’oxydation d’un atome métallique qui n’est pas un élément alcalin ou alcalino-terreux.

Sels de bore

Considérons à titre d’exemple deux sels de bore de formule NaHB₂O₄ et NaH₂BO₄. Pour le premier on a : Ox(Na) = Ox(H) = +I et Ox(O) = -II. Il en découle que 1 + 1 + 2·Ox(B) – 4×2 = 0, soit Ox(B) = 6/2 = +III. Ce nombre d’oxydation est parfaitement normal pour l’atome de bore. Car, il possède 3 électrons de valence. Si l’on applique les mêmes règles au deuxième solide, il vient 1 + 2×1 + Ox(B) – 4×2 = 0. Ici Ox(B) = +V, ce qui impliquerait donc la perte des 2 électrons de l’orbitale 1s de cœur.

Dans ce cas, il est plus raisonnable de penser à un peroxyde où l’oxygène se trouve lié à lui-même. Dans ce cas on aurait Ox(O) = -I au lieu -II. Avec cette nouvelle hypothèse, il vient: 1 + 2×1 + Ox(B) – 4×1 = 0. Soit Ox(B) = +I, ce qui est de nouveau peu probable au vu de la faible électronégativité de l’atome d’oxygène. Donc, la solution vient en considérant que deux atomes d’oxygène ont un nombre d’oxydation de -II. Les deux autres ont alors un nombre d ‘oxydation de -I, soit: 1 + 2×1 + Ox(B) – 2×2 -2×1 = 0. Soit Ox(B) = +III, ce qui est satisfaisant.

Oxydes de fer

Parfois, ce sont les métaux qui peuvent avoir deux degrés d’oxydation différents dans la même structure. Ainsi, pour la magnétite de formule Fe₃O₄, on aurait avec Ox(O) = -II, Ox(Fe) = 8/3 et avec Ox(O) = -I, Ox(Fe) = 4/3, ce qui n’est pas satisfaisant. L’ion peroxyde étant formé de deux atomes d’oxygène chimiquement liés l’un à l’autre [O-O]^2- il est impossible ici que les atomes de fer aient tous le même degré d’oxydation. Toutefois, supposons qu’un atome de fer soit au degré d’oxydation +II et les deux autres au degré d’oxydation +III. Il vient alors : 2 + 3×2 + 4·Ox(O) = 0, soit Ox(O) = -8/4 = -II et tout rentre dans l’ordre.

Complexes de coordination

Il y a aussi les espèces moléculaires contenant des métaux de transition M, appelés complexes de coordination. Il faut ici classer les ligands selon le nombre d’électrons qu’ils peuvent fournir pour se lier avec l’atome métallique central :

Radical simple (1e-) =  X (H, R, Ph, F, Cl, Br, I, OR, NR₂, PR₂, NO, σ-allyl,…)
Ligand monodentate (2e-) = L (:CO, :NR₃, :PR₃, alcènes, :CR₂, alcynes, liaison M-M,…)
Biradical (2e-) = X₂ (=CR₂, =O, =NR, =PR, peroxydes,…)
Ligand radicalaire (3e-) = LX (π-ényl,  ≡CR, =NO, CO₂R, O₂CNR₂,…)
Ligand bidentate (4e-) = L₂ (dioléfines, diphosphines, diamines, diarsines, alcynes, dialcoxyalcanes, liaison M=M,…)
Biradical insaturé (4e-) = LX₂ (:O=, RN:=, RP:=,…)
Radical bidentate (5e-) = L₂X (Cyclopentadiényl, diényl, phospholyl = C₄H₄P,…)
Radical tridentate insaturé (5e-) = LX₃ (≡N:,…)
Ligand tridentate (6e-) = L₃ (benzène, trioléfines, triamines, triphopshines, pyridine, C₅H₅P, liaison M≡M,…)
Biradical bidentate (6e-) = L₂X₂ (porphirines, phtalocyanines,…)
Radical tridentate (7e-) = L₃X (cycloheptatriényl,…)
Ligand tétradentate (8e-) = L₄ (cyclo-octatétraène = COT), liaison quadruple M-M)

Exemple

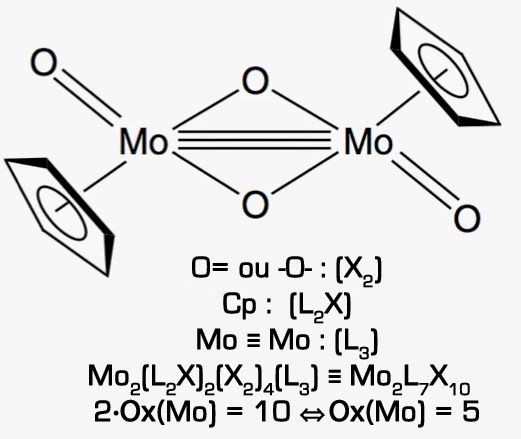
Ce classement préalable ayant été effectué, le complexe peut s’écrire: [ML_nX_m]^Q± ce qui permet de trouver le degré d’oxydation du métal M : Ox(M) = m + Q. Voici un exemple de cette méthode appliquée à un complexe polynucléaire du molybdène de charge nulle (Q = 0). Ainsi, on y trouve deux ligands cyclopentadiényl (Cp) autour d’une liaison triple métal-métal entourés de 4 atomes d’oxygène :