Précession électronique
En février 1926, le physicien britannique Llewellyn Thomas (1903-1992) va pointer une erreur dans le traitement relativiste de l’électron. Ceci permettra de résoudre le problème du facteur 2 dans l’effet Zeeman anormal. Considérons un système de coordonnées où l’électron est momentanément au repos. La fréquence de précession de l’axe du spin de l’électron en présence d’un champ magnétique B vaut :
\begin{cases} \vec{\omega }=\frac{e}{m_{e}}\vec{B} \\\vec{B}=\frac{1}{c^2}\left[\vec{E}\wedge\vec{v}\right ]\end{cases}\Rightarrow\vec{\omega }=\frac{e}{m_{e}c^2}\left[\vec{E}\wedge\vec{v}\right]Ici v désigne la vitesse de l’électron dans le repère où le noyau est au repos. L’expression précédente conduit bien à une séparation du doublet relativiste. Elle est deux fois supérieure à ce que l’on observe expérimentalement. Pour résoudre ce désaccord théorie/expérience, Thomas considère donc un troisième repère. Ce repère est celui où le noyau est au repos. On l’obtient en appliquant une poussée de Lorentz de vitesse :
\vec{a}\cdot dtLa lettre ‘a’ représente l’accélération que subit l’électron suite à son mouvement rotatif autour du noyau. Dans ce nouveau repère, la fréquence de rotation s’exprime comme la somme de deux termes :
\vec{\omega }=\frac{e}{m_{e}}\vec{B}-\frac{1}{2c^{2}}\left [\vec{v}\wedge\vec{a}\right ]Or, l’accélération est, en première approximation, proportionnelle au champ électrique. Il en découle que :
\vec{a}=-\frac{e}{m_{e}}\vec{E}\Rightarrow\vec{\omega}=\frac{e}{m_{e}c^{2}}\left [\vec{E}\wedge\vec{v}\right ]+\frac{1}{2m_{e}c^{2}}\left [\vec{v} \wedge\vec{E}\right ]=\frac{e}{2m_{e}c^{2}}\left [\vec{E}\wedge\vec{v}\right ]Wolgang Pauli
Ceci correspond à la moitié de l’expression où l’on considère l’électron momentanément au repos. L’hypothèse de l’électron en rotation sur lui-même est donc parfaitement compatible avec ce que l’on observe expérimentalement. Elle permet d’expliquer les spectres de structure fine des atomes. Voici d’ailleurs un extrait d’une lettre de Llewellyn Thomas à Samuel Goudsmit. Une telle lettre jette un éclairage intéressant sur la personnalité du physicien Wolfgang Pauli :

Voici une traduction de cette lettre peu élogieuse pour ledit Pauli :
“Je pense qu’Uhlenbeck et toi avaient été très chanceux de voir cette idée de rotation de l’électron sur lui-même publiée et discutée avant que Pauli n’ait été au courant. En effet, il y a un peu plus d’un an, Krönig croyait aussi à une telle précession de l’électron et avait même commencé à écrire quelque chose. Pauli fut la première personne à qui il parla de cette idée. Pauli ridiculisa tellement la chose entière, que la première personne à avoir eu une telle idée fut aussi la dernière et ne voulut plus jamais en entendre parler. Tout ceci pour dire que l’infaillibilité de Dieu ne s’applique en aucune manière à son très autocentré vicaire terrestre.”
De fait, Pauli était célèbre pour ses critiques acerbes et sarcastiques. Ces collègues en étaient même arrivés à le surnommer “La Fureur de Dieu”. Son avis était néanmoins toujours très respecté. Car, Pauli avait, à l’âge de seulement 21 ans, rédigé un traité de physique relativiste de 350 pages. Albert Einstein lui-même n’avait rien trouvé à redire à ce manuscrit. Pour cette raison, il était considéré comme l’égal d’Einstein, voire comme étant supérieur à lui.
Son attitude railleuse et autosuffisante est soulignée par Thomas dans sa lettre à Goudsmit. Cela l’a d’ailleurs conduit à une profonde dépression suite au suicide de sa mère en 1927. Dépression suivie d’un divorce en 1930. Il réussit néanmoins à sortir de cette dépression et à se remarier grâce à l’aide du psychanalyste Carl Gustav Jung. Pauli aida ainsi Jung à découvrir le concept d’inconscient collectif ainsi que le phénomène de synchronicité. Ceci grâce aux rêves que Pauli racontait à Jung dans les moindres détails. Car, Pauli était l’égal d’Einstein pour tout problème lié à la théorie de la relativité. Théorie qui montre que le temps est un concept relatif qui peut être modifié lors de poussées de Lorentz.
Masse relativiste
L’article de Thomas résolvait ainsi le problème de la structure fine des raies d’émission des atomes. Cela permettait aussi d’expliquer l’effet Zeeman anormal. Toutefois, il ne résolvait en rien l’objection de Pauli. Celle-ci concernait les vitesses supralumineuses à la périphérie de l’électron lors de son mouvement de rotation sur lui-même. En fait, là aussi Pauli a été très décevant. Car, son objection à l’idée initiale de Ralph Krönig, était basé sur un calcul très rapide. Calcul qui ne prenait pas en compte la variation de masse de l’électron avec sa vitesse. Pour un spécialiste de la relativité ceci n’est pas très sérieux. Cela démontre, une fois de plus, le caractère hargneux et impulsif de Pauli à cette époque.
Or, on peut montrer que le mouvement de rotation de l’électron sur lui-même conduit bien à un spin demi-entier. Ceci, sans que la vitesse en périphérie ne devienne supralumineuse. Soit donc r la distance à l’axe de rotation. Soit aussi ω la fréquence angulaire de l’électron, d’où une vitesse linéaire v = r·ω. Comme l’avait vu Pauli, cette vitesse augmente donc linéairement avec r. Or, dans le cadre de la théorie de la relativité on a v ≤ c. Toutefois, lorsqu’on arrive en périphérie de l’électron (r = R) on doit avoir, au plus, v = c. Autrement dit, on a que c = R·ω. L’indice de réfraction du vide pour l’onde de matière associée à l’électron vaut donc β = v/c = r/R :
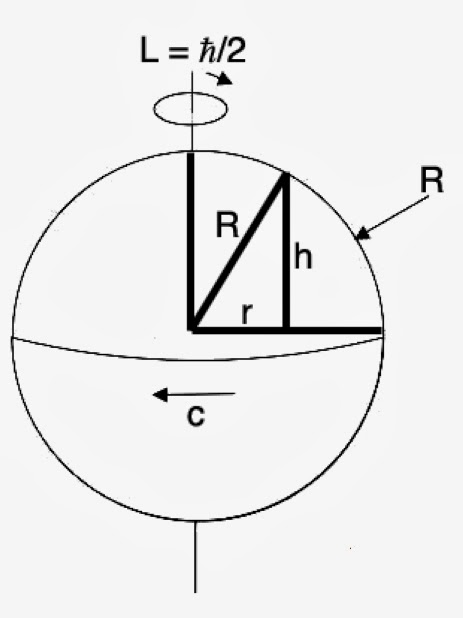
Calcul du spin de l’électron
Ici, la masse m qui est associée à l’électron n’est plus sa masse au repos me. C’est plutôt une masse qui varie avec le facteur β. Ceci permet donc d’exprimer la densité ρ(r) de l’électron en fonction de la distance à l’axe de rotation r. La masse totale de l’électron relativiste se calcule ainsi en intégrant cette densité de masse ρ(r). L’intégration se fait depuis le centre (r = 0) jusqu’à la périphérie (r = R). On considère pour cela un cylindre de circonférence 2πr, de hauteur 2h et d’épaisseur dr :
m(r)=\frac{m_{e}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\Rightarrow m=\int_{0}^{R}\frac{\rho _{e}\cdot 2\pi r\cdot (2h)\cdot dr}{\sqrt{1-\frac{v^{2}}{c^{2}}}}Ici, ρe = me/V, désigne la densité en masse d’un électron. La variable V = (4π/3)·R3 correspond au volume de l’électron. Appliquons le théorème de Pythagore au triangle rectangle de côtés (R, r, h). Il est alors possible d’exprimer la hauteur h en fonction du rapport r/R = v/c, soit :
r^{2} +h^{2}=R^{2}\Rightarrow h=R\sqrt{1-\frac{r^{2}}{R^{2}}}=R\sqrt{1-\frac{v^{2}}{c^{2}}}Ceci permet donc de calculer la masse réelle de l’électron en mouvement relativiste comme :
m=4\pi\rho_{e}\cdot R\int_{0}^{R}r\cdot dr=2\pi\rho _{e}\cdot R^{3}=\frac{3m_{e}}{2}L’électron a donc vu sa masse augmenter de moitié par rapport à sa valeur initiale au repos. Le moment d’inertie I associé à cette masse m en rotation de rayon R, vaut dans ces conditions :
I=4\pi\rho_{e}\cdot R\int_{0}^{R}r^{3}\cdot dr=\pi\rho_{e}\cdot R^{5}=\frac{m\cdot R^{2}}{2}Maintenant, la relation de Planck-Einstein donne la fréquence propre f de l’électron. Fréquence que l’on peut identifier à sa vitesse de rotation angulaire ω, soit :
\omega =2\pi f =\frac{mc^{2}}{\hbar}\Rightarrow R=\frac{c}{\omega }=\frac{\hbar}{mc}=\lambda _{C}On obtient ainsi une taille de l’électron qui est différente de son rayon classique. C’est ce rayon classique qui avait été utilisé par Pauli pour démolir l’idée initiale de Krönig. La nouvelle taille λC s’appelle la longueur d’onde de Compton. Celle-là même qui apparaît dans l’équation de Klein-Gordon et, bien sûr, dans l’effet Compton. Il ne reste plus qu’à calculer le moment angulaire. Il s’obtient en multipliant le moment d’inertie par la vitesse angulaire de rotation ω. Cette vitesse dépend également de la longueur d’onde de Compton de l’électron :
\omega =\frac{c}{\lambda _{C} }\Rightarrow L=I\cdot\omega =\frac{1}{2}mc\cdot\lambda _{C} =\frac{\hbar}{2}Le spin en physique quantique
On trouve donc bien un moment cinétique demi-entier. Ceci valide complètement l’image du spin de l’électron comme un mouvement rotatif de ce dernier sur lui-même. D’ailleurs le même type de calcul peut être mené pour un photon. Cela permet de retrouver très facilement le moment angulaire intrinsèque entier égal à ℏ (et non ℏ/2 comme pour l’électron). Malgré cela, Pauli ne fut jamais totalement convaincu. Il continua à douter de la validité de l’image de l’électron en rotation sur lui-même.
Le scepticisme de Pauli est toujours en vigueur chez beaucoup de physiciens. Ces derniers rechignent à admettre que le grand maître de la théorie de la relativité ait manqué de rigueur. Ceci explique l’auréole de mystère qui continue à entourer la notion de spin dans beaucoup d’ouvrages traitant de physique quantique. Le mythe que le spin est une propriété purement quantique qui n’a aucun équivalent classique persiste donc. Certains pensent ainsi que l’on ne peut exprimer la notion de qu’au moyen de matrices. Comme l’a fait Pauli dans le cadre de la théorie des groupes. Ou bien encore comme l’a fait Paul Dirac en électrodynamique quantique.
Cet état de fait est en partie responsable de la perplexité qu’affichent les personnes non mathématicienne devant la physique quantique. Ce mystère qui a effectivement entouré le spin n’a donc plus de raison d’être de nos jours. Car, la rotation de l’électron autour du noyau entraîne l’existence d’un moment angulaire orbital extrinsèque. De même, la rotation de l’électron sur lui-même engendre un autre type de moment angulaire. Celui-ci est intrinsèque, et s’identifie sans problèmes au spin de la physique quantique.
Références
L. H. Thomas, “The motion of the spinning electron”, Nature, 117 (1926) 514.
M. H. MacGregor, “The Enigmatic Electron”, Kluwer, Dordrecht, 1992.



Leave a Reply