Température et chaleur

Avant 1848, il existait un très grand nombre d’échelles de température empiriques. Puis, William Thomson, futur Lord Kelvin, remarqua que toutes les échelles possibles et imaginables pouvaient être reliées entre elles via des fonctions monotones Θ(θ). Il se posa donc la question de savoir si l’on pouvait en trouver une T(θ) formant un facteur intensif de la chaleur Q. C’est-à-dire, était-il possible de factoriser cette dernière sous la forme δQ = T·dS ? La nouvelle fonction S(U,V) serait alors une variable d’état thermodynamique qui agirait comme une sorte de « volume » pour la chaleur.

Si cela était possible, une telle échelle de température, dite de Kelvin, serait d’une grande utilité théorique. En effet, les lois de la thermodynamique prendraient alors leur forme la plus simple. Or, pour que la fonction S que je cherche soit une fonction d’état, il faut impérativement qu’elle soit une différentielle totale exacte. Car, ceci n’est pas le cas de la différentielle δQ, qui selon le premier principe de la thermodynamique peut s’écrire δQ = dU + p·dV. En effet, si j’intègre cette expression entre deux états d’équilibre 1 et 2, il vient :

\int_1^2 {\delta Q}  = {U_2} - {U_1} + \int_1^2 {p\cdot dV} 

L’intégration du terme dW = p·dV dépend manifestement du chemin connectant l’état initial à l’état final. Ceci signifie tout simplement que la notion de quantité de chaleur Q emmagasinée dans un corps ou de quantité de travail W = p·dV ne sont pas des différentielles totales exactes.

Différentielle totale exacte

En effet, une différentielle totale exacte présente la propriété fondamentale de ne dépendre que de l’état initial et de l’état final. Le chemin suivi entre ces deux états, n’a aucune importance. Or, comme l’a démontré le comte Rumford, on peut tirer par frottement d’un simple canon autant de chaleur que l’on veut (intégrale de δQ). En effet, si je tourne le canon indéfiniment (intégrale de δW), la quantité de chaleur produite sera, elle aussi, infinie. Il en découle que chaleur et travail ne peuvent avoir de différentielle totale exacte.

En fait, comme l’impose le premier principe, la seule quantité bien définie dans un corps, c’est son énergie interne U. Cette dernière se définit comma la somme de la chaleur et du travail mécanique : dU = δQ + δW.

En résumé, on veut que la fonction S(U,V) soit une fonction d’état. C’est-à-dire que sa différentielle soit exacte. Il en découle alors que cette fameuse température de Kelvin T doit être un facteur intégrant de la chaleur. Autrement dit, un facteur multiplicatif qui transforme la différentielle inexacte de chaleur δQ = dU + p·dV en une différentielle totale exacte :

δQ = T·dS ⇒ dS(U,V) = (1/T)·dU + (p/T)·dV.

Dérivées partielles

Or, le problème de trouver un tel facteur intégrant est un problème purement mathématique. Il peut être résolu, indépendamment des propriétés de toute substance particulière. Soit w(U,V) un tel facteur intégrant. Alors le premier principe peut être réécrit :

dS(U,V) = w·dU + w·p·dV

D’où les conditions suivantes :

    w = {\left( {\frac{{\partial S}}{{\partial U}}} \right)_V} = {\left( {\frac{{\partial S}}{{\partial V}}} \right)_U},\frac{{{\partial ^2}S}}{{\partial U\partial V}} = \frac{{{\partial ^2}S}}{{\partial V\partial U}}

On retrouve ici les fameuses dérivées partielles qui fourmillent dans n’importe quel livre de thermodynamique qui se respecte. Ceux qui ne sont pas à l’aise avec cette notion doivent impérativement lire se familiariser avec cette notion. Rappelons pour les étourdis que les deux dérivées premières découlent d’une part, de l’écriture du premier principe exprimé en fonction du facteur intégrant w. D’autre part, elles découlent du fait que l’on considère S comme une fonction de deux variables U et V. Or, on peut écrire, en toute généralité, que pour toute fonction de deux variables f(x,y) on aura :

f(x,y) \Rightarrow df = {\left( {\frac{{\partial f}}{{\partial x}}} \right)_y}\cdot dx + {\left( {\frac{{\partial f}}{{\partial y}}} \right)_x}\cdot dy

Recherche du facteur intégrant

La dernière égalité dans la définition du facteur intégrant w implique des dérivées secondes. Elle garantit le fait que la fonction S sera bien une différentielle totale exacte. C’est-à-dire que l’on pourra donc toujours écrire que : 

\int_1^2 {dS}  = {S_2} - {S_1}

Ceci quel que soit le chemin d’intégration suivi. Appliquons maintenant cette dernière égalité aux deux dérivées premières. Je trouve alors que la fonction w que je recherche doit satisfaire à l’équation :

\frac{{{\partial ^2}S}}{{\partial U\partial V}} = {\left[ {\frac{{\partial w}}{{\partial U}}} \right]_V} = p\cdot{\left( {\frac{{\partial w}}{{\partial U}}} \right)_V} + w\cdot{\left( {\frac{{\partial p}}{{\partial U}}} \right)_V} = {\left( {\frac{{\partial w}}{{\partial V}}} \right)_U} = \frac{{{\partial ^2}S}}{{\partial V\partial U}}

Or, il existe beaucoup de fonctions obéissant à un telle équation. Le plus simple est donc de chercher celles qui que ne dépendent que de la température empirique θ, soit : 

{\left( {\frac{{\partial w}}{{\partial V}}} \right)_U} = \frac{{dw}}{{d\theta }}\cdot{\left( {\frac{{\partial \theta }}{{\partial V}}} \right)_U} = {\mu '_U}\cdot\frac{{dw}}{{d\theta }},{\left( {\frac{{\partial w}}{{\partial U}}} \right)_V} = \frac{{dw}}{{d\theta }}\cdot{\left( {\frac{{\partial \theta }}{{\partial U}}} \right)_V} = \frac{1}{{{{C'}_v}}}\cdot\frac{{dw}}{{d\theta }}

Coefficients thermodynamiques

Ici, pour ne pas alourdir trop l’écriture, j’ai introduit deux coefficients numériques µ’_U et C’_V .Ce sont de simples nombres mesurables expérimentalement. Ainsi, le nombre C’_V s’appelle “capacité calorifique isochore“. De fait, selon sa définition, il correspond à la variation d’énergie interne U lorsque je varie la température θ en gardant le volume constant V. Ce nombre est aisément mesurable si l’on dispose d’un calorimètre travaillant à volume constant. 

Le second coefficient µ’_U s’appelle “coefficient de Joule-Thomson  isoénergétique“. Il indique quelle sera la variation de température θ du système lorsque je varie son volume V à énergie interne U constante. Ce coefficient est aisément mesurable pour des gaz en réalisant une détente de Joule-Gay-Lussac. Ceci consiste à mesurer la variation de température que subit un gaz lorsqu’il se détend dans le vide :

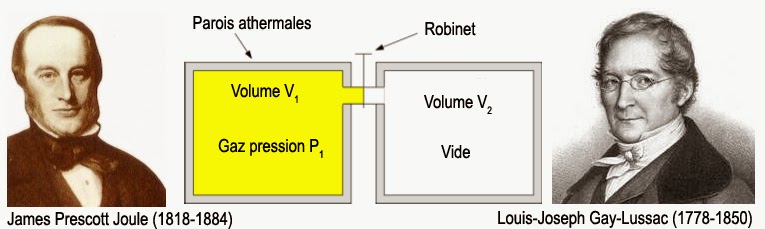
Ici, il n’y a aucun échange de travail ou de chaleur avec l’extérieur. La transformation se fait donc bien à énergie interne constante. D’où l’emploi du qualitatif « isoénergétique ». Si je reporte ces deux expressions dans la condition de différentielle totale exacte, il vient que :

w\cdot{\left( {\frac{{\partial P}}{{\partial U}}} \right)_V} = \frac{{dw}}{{d\theta }}\cdot\left( {{{\mu '}_U} - \frac{p}{{{{C'}_V}}}} \right)\Rightarrow \frac{{dw}}{w} = \frac{{{{\left( {\frac{{\partial P}}{{\partial U}}} \right)}_V}\cdot{{\left( {\frac{{\partial U}}{{\partial \theta }}} \right)}_V}}}{{{{C'}_V}\cdot{{\mu '}_U} - p}}\cdot d\theta\Rightarrow \frac{{d\ln w}}{{d\theta }} = \frac{{{{\left( {\frac{{\partial P}}{{\partial \theta }}} \right)}_V}}}{{{{C'}_V}\cdot{{\mu '}_U} - p}} = \frac{{{{\beta '}_V}}}{{{{C'}_V}\cdot{{\mu '}_U} - p}}

Ici, j’ai introduit le coefficient de pression thermique isochore β’_V. Ce dernier décrit la variation de pression que subit le système lorsque je fais varier sa température en maintenant le volume constant. Supposons maintenant que je change d’échelle de température. Soit τ(θ) la fonction monotone croissante qui permet de passer de l’échelle empirique θ l’échelle empirique τ. Bien évidemment, j’aurais de nouvelles valeurs C’’_V et µ’’_U. Mais, le produit de la capacité calorifique isochore par le coefficient de Joule-Thompson isoénergétique restera le même. Car, en raison de la règle de dérivation en chaîne :

C''_V = {\left( {\frac{{\partial U}}{{\partial \tau }}} \right)_V} = \frac{{d\theta }}{{d\tau }}\cdot{\left( {\frac{{\partial U}}{{\partial \theta }}} \right)_V},{\mu ''_U} = {\left( {\frac{{\partial \tau }}{{\partial V}}} \right)_U} = \frac{{d\tau }}{{d\theta }}\cdot{\left( {\frac{{\partial \theta }}{{\partial V}}} \right)_U} \Rightarrow {C''_V}\cdot{\mu ''_U} = {C'_V}\cdot{\mu '_U}

Soit donc λ = C_V·µ_U – p, cette quantité qui ne dépend pas de l’échelle empirique de température choisie. Le seul terme qui changera dans l’expression précédente sera le numérateur. Soit, toujours en raison de la règle de dérivation en chaîne : 

\frac{{d\ln w(\tau )}}{{d\tau }} = \frac{1}{\lambda }\cdot{\left( {\frac{{\partial P}}{{\partial \tau }}} \right)_V} = \frac{1}{\lambda }\cdot\left( {\frac{{d\theta }}{{d\tau }}} \right){\left( {\frac{{\partial P}}{{\partial \theta }}} \right)_V} = \left( {\frac{{d\theta }}{{d\tau }}} \right)\cdot\frac{{d\ln w(\theta )}}{{d\theta }}

Il en découle que les deux facteurs intégrants ne peuvent différer que par une constante multiplicative : w(τ) = C·w(θ). Ceci correspond à ma liberté de choisir une unité donnée pour mesurer la température. Une fois cette unité fixée, je suis sûr qu’il n’existe qu’une et une seule échelle de température T(θ) = 1/w(θ). Cette fonction unique possède la propriété de transformer la différentielle dS = δQ/T en une différentielle totale exacte.

Échelle de Kelvin

Nous sommes maintenant assurés de l’existence et de l’unicité de cette échelle de température T. On peut se poser maintenant la question de réaliser pratiquement cette échelle de température. Soit donc la transformation où un volume de gaz se détend dans le vide sans changer de température. Pour ce type de transformation, on sait que le coefficient de Joule-Thompson isoénergétique µ’_U s’annule. Dans ces conditions particulièrement simples j’ai λ = -p. Soit, en intégrant la relation précédente entre deux états d’équilibre 1 et 2 :

\int_1^2 {d\ln \left( {\frac{1}{T}} \right)}  = \left[ { - \ln T} \right]_{{T_1}}^{{T_2}} =  - \int_1^2 {\frac{1}{p}} \cdot{\left( {\frac{{\partial p}}{{\partial \theta }}} \right)_V}\cdot d\theta  = \left[ { - \ln p} \right]_{{p_1}}^{{p_2}} \Rightarrow \frac{{{T_2}}}{{{T_1}}} = \frac{{{P_2}}}{{{P_1}}}

Or, les substances qui possèdent un coefficient de Joule-Thompson isoénergétique nul sont appelées “gaz parfaits”. De fait, la plupart des gaz réels se comportent, loin de leur point de condensation, comme des gaz parfaits. Il en découle que pour tout thermomètre basé sur un gaz parfait fonctionnant à volume constant, la pression mesurée sera directement proportionnelle à la température au sens de Kelvin.

Si, on ne souhaite pas travailler à volume constant, il suffit d’exprimer le premier principe au moyen de la fonction d’état enthalpie H. On pourra alors refaire exactement le même raisonnement. Il faudra alors juste introduire de nouveaux coefficients numériques : 

{\alpha '_P} = \frac{1}{V}\cdot{\left( {\frac{{\partial V}}{{\partial \theta }}} \right)_p},{C'_P} = {\left( {\frac{{\partial H}}{{\partial \theta }}} \right)_p},{\mu '_H} = {\left( {\frac{{\partial \theta }}{{\partial p}}} \right)_H}

Le premier coefficient s’appelle coefficient de dilatation thermique isobare. On peut le mesurer au moyen d’un dilatomètre. Le second coefficient s’appelle capacité calorifique isobare. Il se mesure au moyen d’un calorimètre travaillant sous pression constante. Enfin, le dernier terme est le coefficient de Joule-Thompson isenthalpique. Il m’indique quelle sera la variation de température θ du système lorsque je varie sa pression p à enthalpie H constante. Ce coefficient est aisément mesurable pour des gaz en réalisant une détente de Joule-Thomson. On mesure ici la variation de température que subit le gaz dans un tuyau calorifugé où une surpression est compensée par un étranglement. Pour cela, on utilise, en général, une simple bourre de coton :

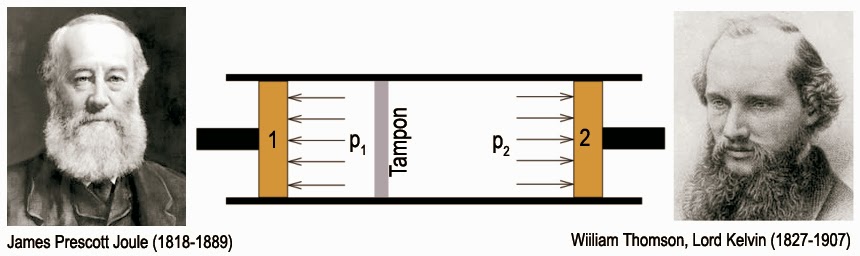
Ici, comme la détente est adiabatique (Q = 0) et que dU = -d(p·V), la transformation se fait bien à enthalpie constante puisque dH = d(U + p·V) = 0. D’où l’emploi du qualitatif « isenthalpique ». De nouveau, toutes les quantités sont primées pour indiquer qu’elles se réfèrent à la température empirique θ. Compte tenu de ces nouvelles définitions, le calcul du facteur intégrant conduira à :

\frac{{d\ln w}}{{d\theta }} =  - \frac{{{{\alpha '}_P}}}{{1 + {{C'}_P}\cdot{{\mu '}_H}/V}}

{\mu '_H} = 0 \Rightarrow \left[ { - \ln T} \right]_{{T_1}}^{{T_2}} =  - \int_1^2 {\frac{1}{V}} \cdot{\left( {\frac{{\partial V}}{{\partial \theta }}} \right)_p}\cdot d\theta  = \left[ { - \ln V} \right]_{{V_1}}^{{V_2}} \Rightarrow \frac{{{T_2}}}{{{T_1}}} = \frac{{{V_2}}}{{{V_1}}}

Par conséquent, soit un thermomètre basé sur une substance ayant un coefficient de Joule-Thompson isenthalpique nul. SI l’instrument fonctionne à pression constante, le volume mesuré sera directement proportionnel à la température au sens de Kelvin. On notera que l’on peut également utiliser n’importe quelle substance. Mais, dans ce cas, il faudra mesurer au laboratoire les coefficients β’_V, C’_V et µ’_U pour le thermomètre travaillant à volume constant. Pour celui travaillant à pression constante, il faudra mesurer les coefficients α’_P, C’_P et µ’_H : 

\frac{{{T_2}}}{{{T_1}}} = \exp \left[ {\int_{{\theta _1}}^{{\theta _2}} {\frac{{{{\beta '}_V}\cdot d\theta }}{{p - {{C'}_V}\cdot{{\mu '}_U}}}} } \right] = \exp \left[ {\int_{{\theta _1}}^{{\theta _2}} {\frac{{{{\alpha '}_P}\cdot\theta }}{{1 + \left( {{{C'}_P}\cdot{{\mu '}_H}/V} \right)}}} } \right]

L’ennui est qu’il faut aussi déterminer comment tous ces coefficients varient avec la température empirique. D’où tout l’intérêt d’utiliser plutôt un gaz parfait. Car, dans ce cas, il suffit juste de mesurer la pression ou le volume pour avoir accès à la température au sens de Kelvin.