Variables intensives et extensives
En thermodynamique on fait la distinction entre deux types de quantités permettant de définir un état donné. Soit un système thermodynamique considéré comme étant composé de plusieurs sous-systèmes, Je trouverais que certaines variables de ce système dites intensives prennent la même valeur dans chacun des sous-systèmes. En revanche, d’autres variables dites extensives se comporteront plutôt de manière additive. Dans ce cas, la valeur totale caractérisant le système est la somme des valeurs trouvées dans chacun des sous-systèmes. Ainsi, la masse est de toute évidence une grandeur extensive. Par contre, à l’équilibre thermique, la température qui la même en tout point est plutôt une variable de nature intensive.
L’énergie est également une grandeur de nature extensive. Mais, ceci n’est vrai que si les différents sous-systèmes n’interagissent pas entre eux. En fait, cette distinction n’a rien de fondamental. Car, c’est à l’expérimentateur qu’il revient en dernier ressort de choisir la manière dont il découpe son système. C’est ce découpage arbitraire qui a pour effet de déterminer quelles seront les variables intensives et extensives.
Pression et volume
Par exemple, un volume d’air pourra être découpé en plusieurs petits volumes contigus dont la somme sera égale au volume total. Dans ce cas, le volume sera une variable extensive. De même, avec une telle partition, la pression sera la même dans chacun des petits volumes. Cette dernière sera donc une variable intensive. Mais, si maintenant je considère que ce même volume d’air est formé de deux types de molécules : oxygène et azote. Le volume occupé par chaque molécule est alors partout le même et le volume devient une variable intensive. Par contre, la pression est égale à la somme des pressions partielles produites par les deux types de molécules. Dans ce cas, la pression qui est additive joue maintenant le rôle de variable extensive.
Un ruban en caoutchouc
Une telle ambiguïté ne peut pas être levée en imposant de ne considérer que des subdivisions purement spatiales. Ceci, de telle manière à ce que chaque sous-système ait la même composition chimique locale. En effet, il suffit de considérer un ruban de caoutchouc élastique en extension. Découpons ce ruban perpendiculairement à son axe en plusieurs bandelettes. Dans ce cas, j’ai une élongation additive, et donc extensive. Par contre, la tension qui est la même dans chaque bandelette sera intensive.
Découpons le même ruban toujours en bandelettes, mais dans le sens de la longueur parallèlement à son axe. L’élongation qui est la même pour chaque bandelette jouera alors le rôle de variable intensive. Par contre, les différentes tensions s’additionnent et deviennent donc extensives. On voit donc que cette distinction entre variables intensives et extensives n’a que peu de sens physique.
Variables conjuguées
Il existe une autre distinction, peut-être un peu plus fondamentale. Elle consiste à les classer les variables thermodynamiques par paires dites “conjuguées”. L’idée est qu’il existe de multiples manières de faire varier l’énergie interne d’un système thermodynamique. Par exemple, plaçons un système de masse m à une hauteur h. On aura alors dans l’énergie interne U un terme m·g·h. Ce terme peut correspondre au produit de la masse par un potentiel de gravitation (g·h). Il peut aussi correspondre au produit d’une force (m·g) par un déplacement h.
Selon le vocabulaire précédemment introduit, masse et hauteur sont des grandeurs extensives. Par contre, potentiel et force sont des grandeurs intensives. Au lieu de cette terminologie, on préférera dire que le couple (masse, potentiel) est une paire de variables conjuguées. Il en est bien sûr de même pour le couple (force, hauteur). Le terme conjugué signifie alors que le produit d’un variable donnée par sa variable conjuguée donne toujours une énergie. Par exemple on dira que volume V et pression p forment un autre paire de variables conjuguées puisque le produit p·V est un travail, forme particulière d’énergie.
Transformées de Legendre
Les transformées de Legendre sont des astuces mathématiques permettant de jongler entre grandeurs extensives et intensives conjuguées ou pas.

Considérons, par exemple, le premier principe sous sa forme la plus simple : dU = dQ – p·dV. Ceci signifie que j’ai deux variables de commandes qui sont la chaleur Q et le volume V. Expérimentalement, je peux travailler, par exemple, à chaleur constante, soit : dQ = 0. On parle alors de conditions adiabatiques. On peut aussi travailler à volume constant, soit : dV = 0. Ceci correspond alors à des conditions isochores. Une conséquence du premier principe est que je ne peux faire varier que deux variables indépendamment l’une de l’autre.
Ainsi, je ne suis plus libre de faire varier arbitrairement une troisième variable P qui est la pression. D’un point de vue théorique cette situation est satisfaisante. Mais, il n’en va pas du tout de même sur le plan pratique. En effet, fixer le volume signifie que le système doit être placé dans une enceinte parfaitement rigide. Cette dernière doit être capable d’encaisser des fortes variations de pression sans se déformer. C’est le protocole expérimental mis en œuvre dans la calorimétrie à volume constant. Cette technique permet de mesurer les variations d’énergie interne au moyen de la capacité calorifique à volume constant CV comme on le voit ici à gauche :
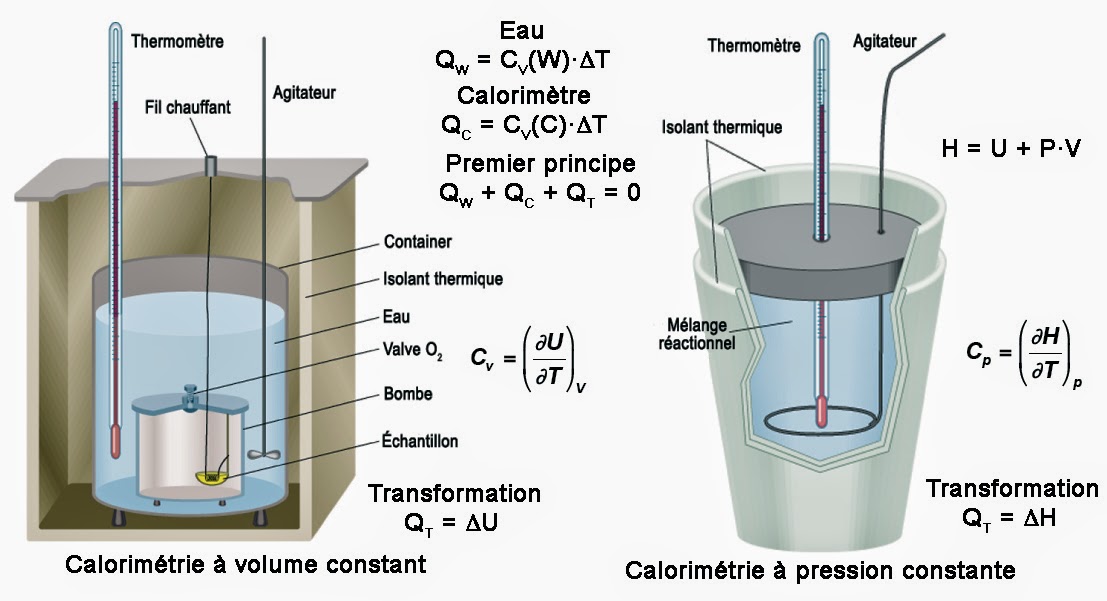
Calorimétrie
Lorsqu’on travaille à volume constant, il se peut que la pression grimpe en flèche. Dans ces conditions, il faut prier pour que le récipient tienne la pression. Car, s’il y a la moindre fissure, le récipient se transformer en une véritable bombe capable de faire voler en éclat tout un laboratoire. Pour cette raison on estime généralement beaucoup plus sûr de travailler à pression constante (dP = 0). Ceci permet au volume de s’adapter aux conditions de pression imposées et le risque d’explosion disparaît. De plus, si la pression fixée par l’atmosphère terrestre, le dispositif expérimental est très simple.
Dans ces conditions de pression fixée, la fonction d’état énergie interne U qui dépend de la chaleur Q et du volume V n’est plus du tout adapté à ce nouveau système thermodynamique. Car, les variables de commandes sont maintenant la chaleur Q et la pression P. Pour remédier à cela, on introduit donc une nouvelle fonction d’état appelée enthalpie H(Q,p). Cette fonction est telle que H = U + p·V. On dit ici que l’enthalpie est la transformée de Legendre de l’énergie interne.
Ceci permet alors d’exprimer le premier principe sous une nouvelle forme différentielle entièrement équivalente à la précédente. Toutefois, les nouvelles variables de commande sont maintenant Q et P, soit :
d(P·V) = P·dV + V·dP et dU(Q,V) = dQ – P·dV ⇒ dH(Q,P) = dU + d(P·V) = dQ + V·dP


Leave a Reply