Le premier principe de la thermodynamique impose que l’énergie totale d’un système reste toujours constante quoi qu’il arrive. Rappelons que l’énergie totale se définit somme de toutes les énergies cinétiques et toutes les énergies potentielles. Ce principe reste parfaitement valable en mécanique quantique. Contrairement au principe d’équipartition de l’énergie qui n’est valable qu’en physique classique. Ce théorème d’équipartition s’intéresse aux formes d’énergie qui font intervenir une fonction quadratique d’un degré de liberté donné q. Il pose ainsi, qu’à l’équilibre thermique, on pourra écrire :

\left\langle {q\cdot\frac{{\partial E}}{{\partial q}}} \right\rangle  = {k_B}T

Ici, T est la température absolue au sens de Kelvin et k_B = 1,380649×10^-23 J·K^-1 est la constante de Boltzmann. La paire de crochets <> désigne la valeur moyenne à l’équilibre. Reste maintenant à identifier tous les types de degrés de libertés q.

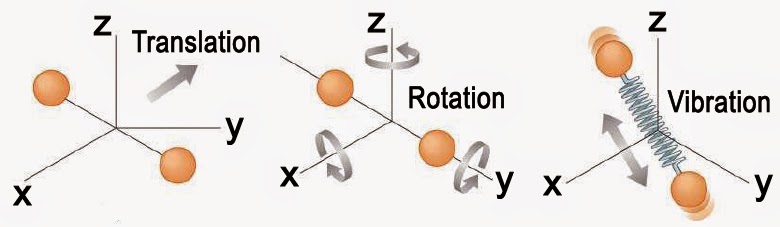
Translations, rotations et vibrations

Considérons à titre d’exemple une molécule diatomique d’hydrogène H₂. On peut considérer que le centre de masse de cette molécule peut se déplacer selon trois directions (X,Y,Z) indépendantes. La molécule peut aussi tournoyer autour de ce même centre de masse selon deux axes. Enfin, elle peut vibrer le long de la liaison H-H de longueur r. Dans ces conditions, l’énergie totale E peut s’écrire :

E = \frac{{p_X^2}}{{2m}} + \frac{{p_Y^2}}{{2m}} + \frac{{p_Z^2}}{{2m}} + \frac{{p_\alpha ^2}}{{2m{r^2}}} + \frac{{p_\beta ^2}}{{2m{r^2}}} + \frac{{p_r^2}}{{2m}} + \frac{1}{2}k\cdot{r^2}

Appliquons le théorème de l’équipartition de l’énergie aux moments linéaires p_i = m·v_i , avec i = X, Y, Z ou r :

\left\langle {{p_i}\cdot\frac{{\partial E}}{{\partial {p_i}}}} \right\rangle  = \left\langle {\frac{{p_i^2}}{m}} \right\rangle  = {k_B}T \Rightarrow \left\langle {\frac{{p_X^2}}{{2m}} + \frac{{p_Y^2}}{{2m}} + \frac{{p_Z^2}}{{2m}} + \frac{{p_r^2}}{{2m}}} \right\rangle  = \frac{{4{k_B}T}}{2} = 2{k_B}T

Pour les deux moments angulaires, chaque contribution vaut aussi de ½k_BT puisque :

\left\langle {{p_\alpha }\cdot\frac{{\partial E}}{{\partial {p_\alpha }}}} \right\rangle = \left\langle {\frac{{p_\alpha ^2}}{{m{d^2}}}} \right\rangle  = \left\langle {{p_\beta }\cdot\frac{{\partial E}}{{\partial {p_\beta }}}} \right\rangle  = \left\langle {\frac{{p_\beta ^2}}{{m{d^2}}}} \right\rangle  = {k_B}T \Rightarrow \left\langle {\frac{{p_\alpha ^2}}{{2m{d^2}}} + \frac{{p_\beta ^2}}{{2m{d^2}}}} \right\rangle  = \frac{{2{k_B}T}}{2} = {k_B}T

Enfin, pour l’énergie potentielle de vibration de la liaison, on aura encore une fois ½k_BT : 

\left\langle {r\cdot\frac{{\partial E}}{{\partial r}}} \right\rangle  = \left\langle {k\cdot{r^2}} \right\rangle  = {k_B}T \Rightarrow \left\langle {\frac{{k\cdot{r^2}}}{2}} \right\rangle  = \frac{{{k_B}T}}{2}

Énergie interne et capacité calorifique isochore

L’énergie interne U de ce gaz s’écrit donc :

U = N_A<E> = 7RT/2 ⇒ C_V = (∂U/∂T)_V = 7R/2

Ici, R = NA·k_B est la constante des gaz parfaits. La physique statistique prévoit ainsi une valeur C_V/R = 7/2 = 3,5 pour le gaz dihydrogène. L’expérience montre que cette valeur n’est atteinte qu’à très haute température. Au voisinage de la température ambiante, une valeur bien plus faible est mesurée. Ceci prouve que la physique classique est foncièrement inapte à décrire le mouvement de la matière. D’où le passage à la physique quantique à l’aube du vingtième siècle.