Attractions et répulsions

Les notions d’énergie cinétique K et d’énergie potentielle U jouent un rôle clef en physique classique ou quantique. Concernant ces deux types d’énergie, l’une s’écrit : K = ½m·v². Ici, m est la masse et v la vitesse d’un mobile donné. Elle est de type répulsif tendant à faire décrire au mobile tout le volume disponible. L’autre U est de type attractive. Elle décrit les forces f qui s’exercent sur le mobile : dU = -f·dr. Le signe moins traduit ici le fait que cette énergie tend à ramener le mobile en un point donné. Ceci l’empêche donc de parcourir tout le volume disponible.

Que peut-on dire maintenant si l’on observe un système matériel possédant une taille caractéristique stable dans le temps ? Il en découle alors nécessairement que les deux contributions K et U se compensent mutuellement. Car, si l’une était vraiment différente de l’autre, on aurait soit un gaz (K >> U), soit un solide compact (K << -U). Ceci signifie donc qu’à l’équilibre thermique il doit exister une relation de dépendance entre K et U. C’est précisément le rôle du théorème du viriel que de préciser une telle relation. Nous démontrons ici ce théorème dans un cadre classique, mais il est bon de savoir qu’il reste parfaitement valable en physique quantique. 

Inversion des vitesses

On considère donc un mobile évoluant dans un volume tridimensionnel restreint de taille r, où r²= x²+ y²+ z². L’idée de base est de considérer le produit scalaire entre le vecteur position et le vecteur vitesse de ce mobile. Comme r est fini, il en découle que la valeur moyenne <x·v_x+ y·v_y+ z·v_z> de ce produit scalaire ne peut être que nulle à l’équilibre thermique. En effet, plaçons-nous en un point de ce volume de coordonnées (x, y, z). Je vais, à un moment donné, voir le mobile s’éloigner de ce point avec une vitesse +v selon la direction x (pour fixer les idées).

Certes, mais restons au même point et attendons suffisamment longtemps. Comme le volume est fini, je serais obligé de voir mon mobile se rapprocher avec la même vitesse. Mais, cette dernière sera orientée cette fois dans la direction opposée -x. Au bilan, j’ai donc <x·v – x·v> = 0. Si d’aventure, le vecteur vitesse ne s’inversait pas dans la direction x, alors cela signifierait que le mobile est perdu à jamais. Mais, ceci est en contradiction avec l’hypothèse de départ selon laquelle le mobile reste confiné dans un volume de taille r. Bien évidemment, ce qui est vrai de la direction x s’applique non seulement aux autres directions y et z, ou bien à n’importe quelle direction spatiale. 

Force dérivant d’un potentiel

Ce point étant acquis, considérons que le mobile se trouve soumis à un potentiel U. Supposons également que ce potentiel soit proportionnel à la taille r du domaine visité élevée à une puissance n, soit U = C·rⁿ. Un tel potentiel pourrait correspondre à une force élastique, auquel cas on aurait n = 2. Il pourrait aussi s’agir d’une force électromagnétique ou gravitationnelle auquel cas on aurait n = -1. Évaluons le produit entre la force f_x= -∂U/∂x qui s’exerce la position en x et dans la direction x. Ici, le symbole ‘∂’ signifie qu’il faut calculer la dérivée du potentiel par rapport à la coordonnée x en considérant que les autres coordonnées y et z sont des constantes. Compte tenu de la forme choisie pour le potentiel U, on a :

{f_x} =  - C\cdot n\cdot{r^{n - 1}}\cdot\frac{{\partial r}}{{\partial x}} =  - n\cdot\frac{U}{r}\cdot\frac{{\partial r}}{{\partial x}}

 Or, rappelons-nous que l’on a r²= x²+ y²+ z² , d’où il vient aussi que :

2r\cdot\frac{{\partial r}}{{\partial x}} = 2x \Rightarrow \frac{{\partial r}}{{\partial x}} = \frac{x}{r}

Il découle de ceci que l’on peut écrire :

x\cdot{f_x} =  - n\cdot U\cdot\frac{{{x^2}}}{{{r^2}}}

 On remarquera aussi que les coordonnées x, y et z jouent un rôle parfaitement symétrique dans l’expression du potentiel U. Le même calcul réalisé dans les directions y et z donnera par analogie directe :

y\cdot{f_y} =  - n\cdot U\cdot\frac{{{y^2}}}{{{r^2}}}   et  z\cdot{f_z} =  - n\cdot U\cdot\frac{{{z^2}}}{{{r^2}}}

Sommons maintenant ces trois expressions. On trouve alors que le produit scalaire entre les vecteurs position et force est proportionnel au potentiel U changé de signe, soit :

x·f_x+ y·f_y+ z·f_z= – n·U·(x²+ y²+ z²)/r²= -n·U

Loi de Newton

Appliquons maintenant la loi de Newton stipulant que le taux de variation de la quantité de mouvement p doit être à tout instant t égal à la force f. Rappelons que la quantité de mouvement est égale au produit de la masse par la vitesse,. On peut donc écrire que pendant un temps dt on aura :

i = (x,y,z) \Rightarrow {f_i} = m\cdot\frac{{d{{\rm{v}}_i}}}{{dt}}

 Évaluons maintenant le produit scalaire entre les vecteurs position et quantité de mouvement. Il vient que :

m·x·dv_x+ m·y·dv_y+ m·z·dv_z = (x·f_x+ y·f_y+ z·f_z)·dt = -n·U·dt

Rappelons également que a dérivée du produit d(f·g) est égale à g·df + f·dg, soit :

 m·d(x·v_x+ y·v_y+ z·v_z) = m·(dx·v_x+ dy·v_y+ dz·v_z) + (m·x·dv_x+ m·y·dv_y+ m·z·dv_z)

On sait que le deuxième terme à droite dans cette relation est égal à -n·U·dt. Or, par définition du vecteur vitesse on a dx = v_x·dt, dy = v_y·dt et dz = v_z·dt. Compte tenu du fait que l’énergie cinétique s’écrit K = ½m·v², on en déduit que :

m·d(x·v_x+ y·v_y+ z·v_z) = [m·(v_x²+ v_y²+ v_z²) – n·U]·dt = (m·v²– n·U)·dt = (2K – n·U)·dt

Il reste maintenant à attendre suffisamment longtemps pour s’assurer que la condition de mouvement dans un volume restreint <x·v_x+ y·v_y+ z·vz> = 0 soit satisfaite pour trouver que 2·<K> = n·<U>.

Théorème du viriel

Voici donc l’expression du théorème du viriel : 

Soit un système matériel soumis à un potentiel variant comme la puissance n de la distance r à l’origine. Si ce système reste confiné à tout moment dans un volume de taille finie, il existe une condition d’équilibre mécanique statistique. Cette condition est que le double de la valeur moyenne de l’énergie cinétique <K> sera égale à n fois la valeur moyenne de l’énergie potentielle <U>, soit 2<K> = n·<U>.

Notons bien que ce théorème concerne le comportement du système au bout d’un temps infini. On ne peut rien savoir de son comportement à un instant t. Il peut s’appliquer dans toute situation où le système adopte une taille caractéristique. Et, ce quel que soit le nombre d’objets constitutifs. Il s’applique donc aussi bien à un atome, qu’à une protéine, un cristal, une cellule, une planète, un système stellaire, une galaxie, même à un amas de galaxie. Peu importe la taille du système pourvu que cette taille soit stable dans le temps.

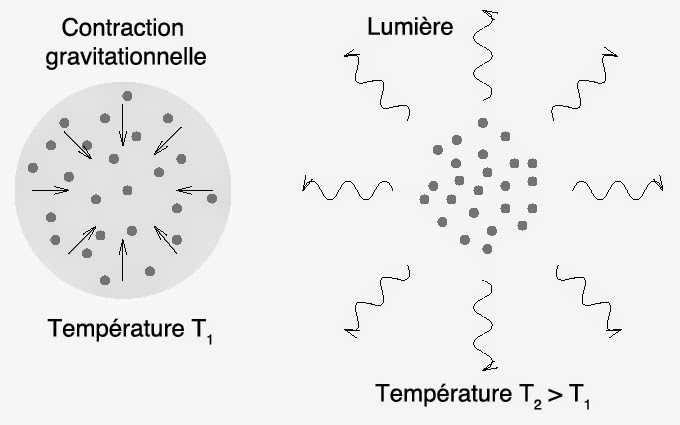
Application une étoile

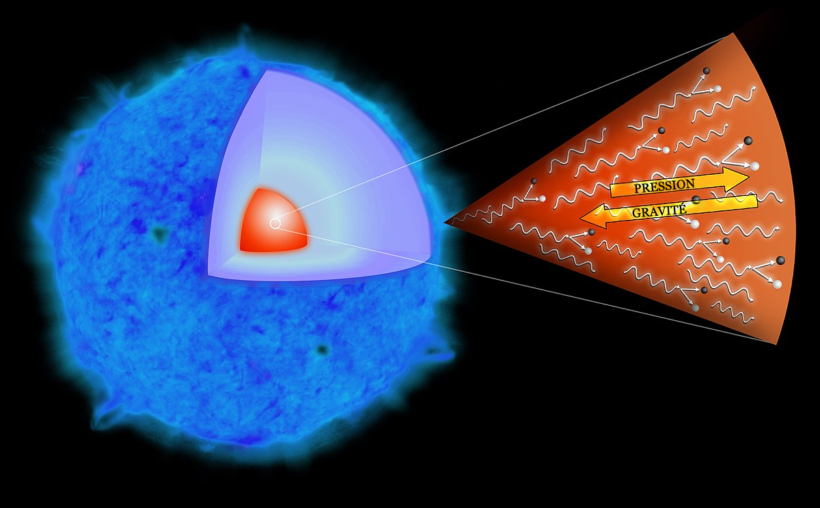
Le théorème du viriel permet, par exemple, de comprendre ce qui se passe lorsqu’une masse de gaz se contracte. Ainsi, la moitié de l’énergie potentielle acquise sert à réchauffer l’étoile. Tandis que l’autre moitié est émise sous forme de lumière. En effet, soit une masse M de gaz assimilable à une sphère de rayon R contenant N particules en mouvement. La loi de gravitation universelle de Newton nous apprend qu’il possède une énergie potentielle U :

U = {\rm{ - G\cdot}}\frac{{{M^2}}}{2R}

On constate que l’énergie potentielle variant comme R^-1. Nous avons donc dans le cas présent n = -1. Et, le théorème du viriel nous apprend que si cette masse de gaz garde une taille finie, l’énergie cinétique moyenne doit valoir :

\left\langle K \right\rangle = \frac{3}{2}N\cdot{k_B}T = - \frac{{\left\langle U \right\rangle }}{2} = G\cdot\frac{{{M^2}}}{{4R}} \Rightarrow R\cdot T = G\cdot\frac{{{M^2}}}{{6N\cdot{k_B}}}

Ainsi, pour une masse M et un nombre N fixé, le produit du rayon par la température doit rester constant. Si le nuage de gaz se contracte suite à l’attraction gravitationnelle entre les particules, R diminue. Par conséquent, T doit augmenter afin de que le produit R·T reste constant. Cette augmentation de température provoque ainsi une augmentation de la luminosité de la masse gazeuse. Car, comme le stipule la loi de Wien, on a λ_max·T = 2898 µm·K. De même, pour la loi de Stefan, on a P = σ·T⁴, avec σ = 5,67·10^-8 W·m^-2·K^-4.

Galaxies

C’est ainsi que se forment et brillent dans le ciel toutes les étoiles et galaxies. Le théorème du viriel permet aussi connaissant la vitesse moyenne V des étoiles tournant autour du centre de leur galaxie de remonter à la masse totale présente :

2\left\langle K \right\rangle  = M\cdot{V^2} = G\cdot\frac{{{M^2}}}{{2R}} \Rightarrow M = \frac{{2R\cdot{V^2}}}{G}

Prenons la masse du soleil M_S = 1,98·10³⁰ kg comme référence et exprimons la distance en parsecs,1 pc= 3,085 678·10¹⁶ m = 3,2616 années-lumière. Il vient donc que :

\frac{M}{{{M_S}}} = 467\cdot{\left[ {V/km\cdot{s^{ - 1}}} \right]^2}\cdot\left[ {R/a.l.} \right]

Ainsi, on sait par décalage Doppler que le soleil se trouve à une distance de 8500 pc  du centre de la Voie lactée. On sait aussi qu’il se délace avec une vitesse voisine de 220 km·s^-1. Il en découle donc que la masse de la Voie lactée vaut environ 1,9·10¹¹ masses solaires.