Définition

Il est facile de se convaincre que toute substance présente en elle-même une tendance au changement qui peut se manifester de plusieurs manières [1] :
i) par réaction avec une autre substance (chimie)
ii) par transformation dans un autre état d’agrégation (thermodynamique)
iii) par migration vers un autre lieu (mécanique)

Comment mesurer cette tendance au changement propre à une substance donnée ? C’est précisément le rôle du potentiel chimique µ de répondre à une telle question. On peut montrer que ce potentiel chimique dépend de la température, de la pression, de l’état d’agrégation (gaz, liquide, solide). Il peut même aussi dépendre de la nature du solvant dans le cas des solutions. Sur un plan de causalité, on peut dire qu’un changement peut se produire dès que le potentiel chimique µ dans l’état initial A est supérieur au potentiel chimique de l’état final B.

Trois cas de figure

Muni de cette notion de potentiel chimique, on peut se retrouver dans 3 situations :

i) µ_A > µ_B, ce qui signifie que l’état A se caractérise par une tendance spontanée à se transformer en l’état B. Pour un équilibre mécanique, cela signifie que A présente une tendance spontanée à se déplacer du point A vers le point B.

ii) µ_A = µ_B, ce qui signifie que rien ne se passe, ni transformation, ni transport. Cette égalité est, de fait, la condition d’équilibre vis-à-vis de toute variation de nombre de moles n.

iii) µ_A < µ_B, ce qui signifie que l’état B présente une tendance spontanée à se transformer en l’état A. Pour un équilibre mécanique, cela signifie que A présente une tendance spontanée à se déplacer du point B vers le point A.

On notera que les états, A, ou B n’ont pas besoin de correspondre à des substances pures. Il peut très bien s’agir de mélanges, d’alliages ou de solutions. De manière plus générale, la notion s’applique à tout ensemble de substances présentant des environnements distincts. L’unité de potentiel chimique est le joule par mole de substance (J·mol^-1).

Relation avec les potentiels thermodynamiques

Sur un plan technique, il est possible de changer l’énergie U d’un système de multiples façons. On peut ainsi faire varier l’entropie S, le volume V, le nombre de moles n, la charge électrique Q, la quantité de mouvement, la masse m, le moment cinétique L, l’aire A, le moment dipolaire électrique P ou le moment dipolaire magnétique M :

dU = T\cdot dS - p\cdot dV + \mu \cdot dn + \varphi \cdot dQ + {\rm{\vec v\cdot d\vec p}} + \psi \cdot dm + \vec \omega \cdot d\vec L + \gamma \cdot dA - \vec E\cdot d\vec P - \vec B\cdot d\vec M

À chaque variation infinitésimale d’une quantité extensive, correspond une quantité de nature intensive. Celle-ci ne dépend pas de la taille du système. Ici, les variables intensives sont : température T, pression p, potentiel chimique µ, potentiel électrique φ, vitesse v, potentiel gravitationnel ψ, vitesse angulaire ω, énergie interfaciale γ, champ électrique E et champ magnétique B. Pour un système où les variables extensives se limitent à l’entropie, le volume et au nombre de moles, la relation précédente se réduit à :

\mu  = {\left( {\frac{{\partial U}}{{\partial n}}} \right)_{S,V}} = {\left( {\frac{{\partial H}}{{\partial n}}} \right)_{S,p}} = {\left( {\frac{{\partial F}}{{\partial n}}} \right)_{T,V}} = {\left( {\frac{{\partial G}}{{\partial n}}} \right)_{T,p}}

Les autres relations impliquent l’enthalpie H, l’énergie libre d’Helmholtz F et l’énergie libre de Gibbs G. Elles découlent des définitions H = U + p·V, F = U – T·S et G = H – T·S. Ces relations montrent tout l’intérêt de la notion de potentiel chimique. En effet, sa définition ne dépend du type de potentiel thermodynamique qui atteint une valeur minimale à l’équilibre.

Potentiel chimique de l’eau

D’un point de vue pratique, la valeur absolue du potentiel chimique importe peu. Les chimistes ont ainsi convenu que le potentiel chimique d’un élément dans sa forme la plus stable sous une température et une pression standard était nul (échelle conventionnelle). Un choix moins arbitraire consisterait à considérer que le potentiel chimique s’annule pour des atomes dans leur état d’énergie minimal (échelle atomique). En règle générale une substance est d’autant plus stable que son potentiel chimique est plus bas. Ceci signifie que les substances qui, sur l’échelle conventionnelle, ont un potentiel chimique positif présentent une tendance spontanée à se décomposer en leurs éléments constituants. Ce sont donc des substances qui sont généralement difficiles à isoler et à conserver.

Par exemple, le potentiel chimique de l’eau sous forme de glace vaut µ(glace) = -236,59 kJ·mol^-1. Si cette eau est à l’état liquide, son potentiel chimique s’abaisse : µ(liq.) = -237,18 kJ·mol^-1. Enfin, pour de la vapeur d’eau, on a µ(vap.) = -228,59 kJ·mol^-1. Ces valeurs sont valables pour une température T = 25°C et à pression atmosphérique. Ces trois valeurs indiquent que l’eau est stable par rapport à sa décomposition en oxygène gazeux (O₂) et hydrogène gazeux (H₂). Car, par définition, on a µ(O₂) = µ(H₂) = 0. On voit aussi que dans cet état standard, c’est le liquide qui possède le potentiel chimique le plus bas.

Potentiels chimiques d’autres substances

En revanche, les potentiels chimiques de l’acétylène C₂H₂ ou du benzène C₆H₆ sont positifs avec µ(C₂H₂)  = +209 kJ·mol^-1 et µ(C₆H₆)  = +125 kJ·mol^-1. Ces valeurs pointent vers une instabilité intrinsèque de ces molécules par rapport à un mélange de graphite caractérisé par µ(C) = 0 et d’hydrogène gazeux. On remarquera ici que cette instabilité thermodynamique ne signifie pas pour autant que la substance ne pourra pas être synthétisée. Car, une fois fabriquée elle peut se trouver dans un état métastable. Elle peut de fait rester indéfiniment dans un tel état, si l’énergie d’activation pour la transformation est trop grande par rapport à la température disponible.

Effet de la température et de la pression

D’un point de vue pratique, il est important de connaître aussi les coefficients de variation du potentiel chimique en fonction de la température ou de la pression. Lorsque les intervalles de température sont faibles, une approximation linéaire permet alors de savoir comment variera le potentiel chimique :

{\alpha _\mu } = {\left( {\frac{{\partial \mu }}{{\partial T}}} \right)_{p,n}} \Rightarrow \mu (T) \approx \mu ({T_0}) + {\alpha _\mu }\cdot(T - {T_0})

{\beta _\mu } = {\left( {\frac{{\partial \mu }}{{\partial p}}} \right)_{T,n}} \Rightarrow \mu (p) \approx \mu ({p_0}) + {\alpha _\mu }\cdot(p - {p_0})

La signification physique de ces deux coefficients peut être comprise en considérant la différentielle de la fonction énergie libre de Gibbs, qui pour un jeu de variable (p, T, n) s’écrit :

dG = V\cdot dp - S\cdot dT + \mu \cdot dn \Rightarrow V = {\left( {\frac{{\partial G}}{{\partial p}}} \right)_{T,n}}, - S = {\left( {\frac{{\partial G}}{{\partial T}}} \right)_{p,n}},\mu  = {\left( {\frac{{\partial G}}{{\partial n}}} \right)_{T,p}}

Grâce à ces relations, on peut montrer que le coefficient de variation du potentiel chimique en fonction de la pression correspond au volume molaire partiel. Dans le cas d’une substance pure, ceci correspond au volume occupé par une mole de substance V/n :

{\beta _\mu } = {\left( {\frac{{\partial \mu }}{{\partial p}}} \right)_{T,n}} = {\left[ {\frac{\partial }{{\partial p}}\left\{ {{{\left( {\frac{{\partial G}}{{\partial n}}} \right)}_{T,p}}} \right\}} \right]_{T,n}} = {\left[ {\frac{\partial }{{\partial n}}\left\{ {{{\left( {\frac{{\partial G}}{{\partial p}}} \right)}_{T,n}}} \right\}} \right]_{T,p}} = {\left( {\frac{{\partial V}}{{\partial n}}} \right)_{T,p}} = {\rm{\bar v}}

De même, peut montrer que le coefficient de variation du potentiel chimique en fonction de la température correspond à l’opposé de l’entropie molaire partielle. Dans le cas d’une substance pure, ceci correspond l’entropie d’une mole de substance -S/n :

{\alpha _\mu } = {\left( {\frac{{\partial \mu }}{{\partial T}}} \right)_{p,n}} = {\left[ {\frac{\partial }{{\partial T}}\left\{ {{{\left( {\frac{{\partial G}}{{\partial n}}} \right)}_{T,p}}} \right\}} \right]_{p,n}} = {\left[ {\frac{\partial }{{\partial n}}\left\{ {{{\left( {\frac{{\partial G}}{{\partial T}}} \right)}_{p,n}}} \right\}} \right]_{T,p}} = {\rm{ - }}{\left( {\frac{{\partial S}}{{\partial n}}} \right)_{T,p}} = -{\rm{\bar s}}

Graphite et diamant

Pour illustrer l’intérêt de ces coefficients, considérons le cas du carbone solide. Dans sa forme “graphite”, il se caractérise par µ_g = 0, α_g = 5,74 J·mol-1·K^-1 et β_g = 5,41 cm³·mol^-1. Dans sa forme “diamant”, on a plutôt µ_d = 2900 J·mol^-1, α_d = 2,38 J·mol^-1·K-1 et β_d = 3,42 m³·mol^-1. On voit que dans ces conditions standard, le potentiel chimique du diamant est, hélas, positif. Ceci signifie que c’est la forme graphite qui est la forme la plus stable. Car, tout simplement, son potentiel chimique est plus bas. On voit aussi que le graphite possède une entropie plus haute et contient plus de vide que le diamant. Essayons d’estimer à quelle température les deux phases pourront être en équilibre. Il suffit pour cela d’écrire l’égalité des potentiels chimiques :

{\mu _g}({T_0}) + {\alpha _g}(T - {T_0}) = {\mu _d}({T_0}) + {\alpha _d}(T - {T_0}) \Rightarrow T - {T_0} = \frac{{{\mu _d}({T_0}) - {\mu _g}({T_0})}}{{{\alpha _g} - {\alpha _d}}} = 860K

De même, cherchons la pression approximative à laquelle les deux phases seront en équilibre. Ici aussi, il suffit d’écrire à nouveau l’égalité des potentiels chimiques :

{\mu _g}({p_0}) + {\beta _g}(p - {p_0}) = {\mu _d}({p_0}) + {\beta _d}(p - {p_0}) \Rightarrow p - {p_0} = \frac{{{\mu _d}({p_0}) - {\mu _g}({p_0})}}{{{\beta _g} - {\beta _d}}} = \frac{{2900}}{{1,99\cdot{{10}^6}}} = 1,5&nbsp GPa

Rappelons que 1 bar = 10⁵ Pa. Il faudra donc une pression minimale de 15 kbar et une température de l’ordre de 600°C pour espérer voir le graphite se transformer en diamant.

Mesure du potentiel chimique

D’un point de vue expérimental, le potentiel chimique se mesure au moyen d’une cellule à combustion fonctionnant de manière réversible.

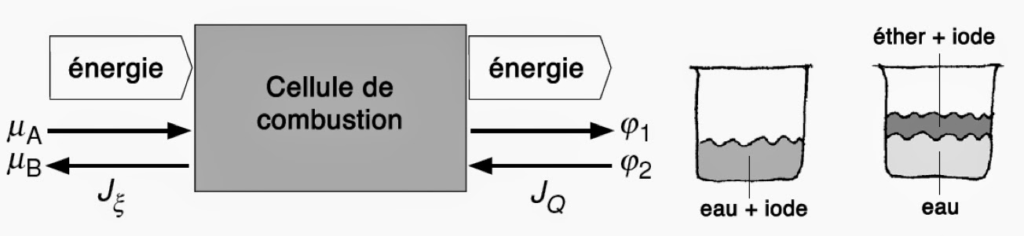
D’après la loi de conservation de l’énergie, la puissance électrique dissipée dans la cellule est égale au produit du flux de charge J_Q par la chute de potentiel électrique (φ₁ – φ₂). Égalisons cette puissance à la puissance chimique qui correspond au produit de la vitesse de transformation J_ξ par la différence de potentiel chimique (µ_A – µ_B). Or, le flux de charge électrique est couplé à la vitesse de transformation via le nombre d’électrons transférés z et la constante de Faraday F = N_A⨯e = 96 500 C·mol^-1 :

({\varphi _1} - {\varphi _2})\cdot{J_Q} = ({\mu _A} - {\mu _B})\cdot{J_\xi } \Rightarrow ({\mu _A} - {\mu _B}) = z\cdot F\cdot({\varphi _1} - {\varphi _2})

On voit donc que mesurer un potentiel chimique revient à mesurer une tension électrique. Ceci aux bornes d’un circuit ouvert dont la résistance en charge est grande par rapport à la résistance interne de la cellule. 

Variation en fonction du nombre de moles

Il existe également une loi de variation du potentiel chimique en fonction du nombre de moles à température et volume constant. Cette loi s’applique à condition que l’équilibre chimique soit établi. Il faut donc qu’il n’y ait aucun obstacle au niveau des échanges de matière :

\mu (n) - \mu ({n_0}) = RT\cdot\ln \left( {\frac{n}{{{n_0}}}} \right)

Beaucoup de lois peuvent être dérivées de cette relation. Elle sous-tend, par exemple, la loi des gaz parfaits. Pour les solutions, on dérive la loi de Raoult ou la loi de Henry. Pour les transferts d’électrons, on obtient la loi de Nernst. Dans le cas des transformations physiques, on obtient l’équation de la pression de vapeur. Enfin, pour les transformations chimiques, on aura la loi de van’t Hoff ou la loi de Boltzmann. Par exemple, pour ce qui concerne la loi des gaz parfaits, on peut écrire compte tenu du fait que la pression est proportionnelle au nombre de moles :

P \propto n \Rightarrow \mu (P) - \mu ({P_0}) = RT\cdot\ln \left( {\frac{P}{{{P_0}}}} \right) \Rightarrow {\left( {\frac{{\partial \mu }}{{\partial P}}} \right)_{T,n}} = \frac{V}{n} = \frac{{RT}}{P} \Leftrightarrow P\cdot V = n\cdot RT

Cette relation nous montre que le potentiel chimique augmente avec la pression. C’est la raison pour laquelle on considère généralement qu’une différence de pression est la force motrice pour initier un flux de liquide et de gaz. De la même manière on considérera qu’un gradient de concentration est la force motrice pour la diffusion de matière. Il est important de bien réaliser que la force motrice n’est pas le gradient de pression ou de concentration, mais bien le gradient de potentiel chimique.

Transitions de phases

Une transition de phase constitue un cas particulier de réaction chimique. En effet, dans ce cas, il n’y a qu’un seul réactif A et un seul produit B. Cette particularité est souvent utilisée pour qu’une réaction soit qualifiée de physique plutôt que de chimique. Évidemment, sur un plan formel, cette distinction est parfaitement inutile. Par analogie avec une réaction chimique, on aura donc les situations suivantes :

i) µ_A > µ_B, ce qui signifie que la phase A présente une tendance spontanée à se transformer en la phase B.
ii) µ_A = µ_B, ce qui signifie que les phases A et B sont en équilibre.
iii) µ_A < µ_B, ce qui signifie que la phase B présente une tendance spontanée à se transformer en la phase A.

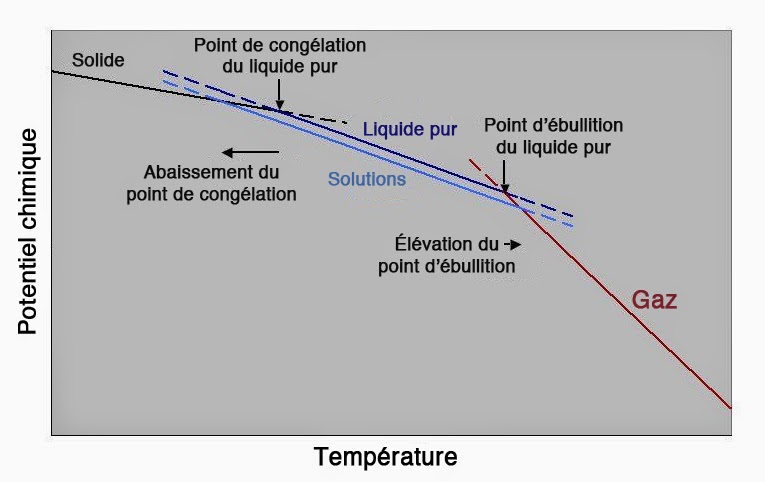
Rappelons que le potentiel chimique dépend de la température et de la pression. Tout changement de l’une de ces deux quantités peut donc provoquer un changement de phase. Pour toutes les phases qui possèdent une entropie molaire positive, il y aura décroissance du potentiel chimique lorsque la température augmente. En particulier, la décroissance la plus forte sera observée dans le cas des gaz, les liquides ayant eux-mêmes une décroissance plus forte que les solides. On doit donc s’attendre à ce que les courbes µ = f(T) de deux phases différentes auront forcément une intersection. Ainsi pour l’eau et pour la glace sous une pression de 1 bar, l’intersection se produit à une température T = 273K = 0°C.

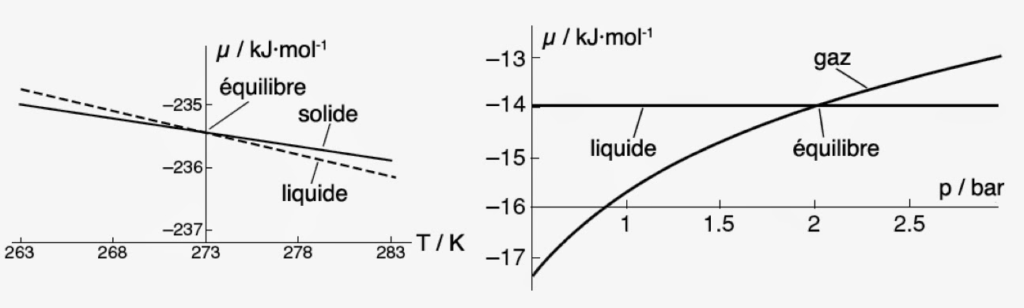
À cette température, le potentiel chimique de la glace est exactement égal au potentiel chimique du liquide. Car, en ce point les deux phases coexistent et sont en équilibre chimique.

Pression et point de fusion

Le potentiel chimique dépend aussi de la pression. Il en découle que la position de l’intersection entre glace et liquide variera aussi avec la pression. En d’autres termes, le point de fusion d’une substance dépend de la pression. Le volume molaire étant une quantité positive, le potentiel chimique augmentera toujours avec la pression quel que soit l’état d’agrégation de la substance (gaz, liquide ou solide).

Les courbes µ = f(p) d’une même substance pouvant exister sous deux phases différentes se croiseront donc à une certaine pression. Les transitions solide ↔ liquide ↔ gaz ont ceci de particulier que leurs énergies d’activation respectives sont en général pratiquement nulles. Il est par conséquent très difficile d’établir une différence de potentiel chimique entre deux phases. De la même manière qu’il est très difficile d’établir une différence de potentiel électrique entre deux corps reliés par un fil conducteur. En effet, même si l’on arrive à déposer une charge électrique sur l’un des deux corps, aucune différence de potentiel électrique ne se manifestera. Car, la charge va se redistribuer rapidement pour égaliser les potentiels.

Métastabilité

C’est pour cette raison que dans des conditions de température et de pression données, une substance existera sous un état d’agrégation bien défini. Par exemple, l’eau à pression ambiante sera sous forme liquide à condition que sa température soit comprise entre °C et 100°C. Elle deviendra gazeuse dès que T > 100°C. Toutefois, si l’on travaille dans des conditions particulières (four à microöndes par exemple), il sera possible d’obtenir de l’eau liquide surchauffée. Dans cet état dit métastable (T > 100°C), le potentiel chimique du liquide est supérieur à celui de la vapeur.

Le fait que la transition se produise à une température plus haute que prévu nous surprend tellement que l’on donne un nom particulier à ce type de situation. En fait, dans le cas d’une transformation chimique, comme dans le cas de la réaction entre H₂ et O₂, l’absence de transition ne surprend pas outre mesure. On invoque alors la présence d’une barrière d’activation pour expliquer le phénomène. Il en est de même ici. Le fait que l’on puisse obtenir de l’eau liquide “surchauffée”, indique que dans le liquide, quelque chose s’oppose à la transformation. Les chimistes invoquent dans ce cas, la présence de liaisons hydrogène entre les molécules d’eau.

Potentiel chimique et courants

Plus haut, le potentiel chimique a été interprété comme la force motrice. Ceci afin que le nombre de moles d’une substance donnée puisse varier. Or le nombre de moles n’est qu’une variable extensive parmi d’autres. Il y a aussi la masse, la charge électrique, l’entropie ou le moment cinétique. Supposons qu’il y ait un couplage entre le nombre de moles et l’une de ces variables extensives. Il s’ensuit que le flux de la substance pourra aussi être piloté par la grandeur intensive qui est conjuguée à la variable extensive couplée. Plus fort sera le couplage, plus efficace sera l’entraînement.

De fait, masse et charge électrique sont toujours couplés de manière extrêmement rigide au nombre de moles n. En effet, si M désigne la masse molaire, on aura la relation J_m = M·J_n entre le courant de masse J_m et le courant de moles J_n. Pour les réactions d’oxydo-réduction, on aura également le couplage rigide J_Q = z·F·J_n entre le courant de charge électrique J_Q et le courant de moles J_n. D’autres couplages sont nettement moins rigides. C’est le cas des objets de masse importante. Ici, l’existence d’un champ de gravitation ψ fait que le potentiel pertinent total γ est la somme du potentiel chimique et du potentiel gravitationnel : γ = µ + M·ψ. Dans ces conditions le flux de substance sera nul lorsque la condition γ = 0 sera satisfaite, même si les gradients individuels ne sont pas nuls.

Potentiel électrochimique

C’est en particulier la raison pour laquelle, la masse d’eau au fond d’un verre ne cherche pas à remonter vers la surface. Bien que ce soit la direction qui favorise une diminution de son potentiel chimique. Pour la même raison, l’eau en haut du verre ne cherche pas redescendre malgré le fait que ce mouvement entraîne un abaissement de son potentiel gravitationnel. En fait, l’eau du verre est soumise à deux types de forces motrices chacune non nulles. Mais, ces forces s’opposent et se compensent exactement. Ceci fait que le potentiel gravito-chimique s’annule en tout point et à tout moment.

Le même type de raisonnement s’applique aux charges électriques via la définition d’un potentiel électrochimique η = µ + z·F·φ. Ici, on a la condition de courant électrique nul dès que η = 0. Ainsi, le potentiel chimique des porteurs de charge n’est pas le même dans deux métaux comme le cuivre et l’argent. Dès que je mets en contact ces deux métaux, les porteurs de charge se déplacent de manière à générer une différence de potentiel non nulle. Cette dernière est fonction de la différence qui existe entre les potentiels chimiques respectifs. À l’équilibre aucun courant ne circule, car le potentiel électrochimique est le même dans les deux matériaux. Et, ce bien qu’il existe au voisinage de l’interface une charge d’espace.

Électronégativité des atomes

L’atmosphère est un exemple où la force motrice ε pour le déplacement des masses d’air est la combinaison de trois potentiels différents : ε = µ + M·ψ + s·T. On parle alors de (potentiel gravito-thermo-chimique). Pour être complets, signalons que la notion de potentiel chimique existe également dans les atomes. On parle alors d’électronégativité, potentiel qui gouverne les transferts d’électrons entre orbitales comme le potentiel chimique  gouverne les transferts de moles entre les phases. En fait, tout déplacement de matière, d’énergie ou de charge se traite via un potentiel qui prend à l’équilibre la même valeur en tout point du système.

Références

Job G. & Herrmann F. (2006), «Chemical potential – a quantity in search of recognition», Eur. J. Phys., 27, 353-371.