Introduction
Dans la chronique n° 78, j’ai développé l’idée que l’être humain formait un système « complexe ». Ceci, par opposition aux machines qui sont, elles, des systèmes compliqués. Une machine peut donc être démontée, puis remontée. Elle survivra à l’opération. Un être humain, lui, décédera. Et, si on cherche à le remplacer par un nouvel être humain, ce dernier sera nécessairement différent de celui qui vient de disparaître. Alors qu’une nouvelle machine, sera parfaitement indiscernable de la machine qu’elle remplace. Voilà une première idée. Ensuite, j’ai exprimé quelques généralités sur les nombres 0 (rien), 1 (tout), 2 (dualité instable) et 3 (trinité stable). Et, je vous ai proposé d’aller encore plus en profondeur…
Ce que je ferai maintenant. Avant cela, je vous informe que trois livres m’ont considérablement aidés pour explorer la profondeur des nombres. Le premier est un manuscrit posthume du « Philosophe inconnu », Louis-Claude de Saint-Martin (1743-1803). Une édition récente du texte intégral du manuscrit original permet d’avoir accès à une sagesse qui remonte à l’Égypte ancienne [1]. Le second livre est celui du mathématicien Ernst Bindel (1890-1974), qui s’est, lui aussi, intéressé de très près à la sagesse antique égyptienne [2]. Le dernier est le livre de François-Xavier Chaboche, est, lui, plus tourné vers le symbolisme, voire l’ésotérisme [3].
Une approche qualitative
En effet, dès que l’on souhaite saisir le développement de la pensée humaine dans toute son ampleur, il est très difficile de remonter le temps au-delà de l’Égypte ancienne. Certains pourront se demander, à juste titre, pourquoi se préoccuper de modes de pensées très primitifs. Alors que nous disposons d’une science moderne extrêmement performante. La réponse à cette question tient au fait que la science moderne a complètement occulté le fait qu’un être humain n’est pas uniquement fait de matière. Si tel était le cas, il n’y aurait dans notre existence, aucune âme, aucune poésie, aucun art, aucun amour.
On en revient donc à la nécessité d’une alchimie entre les côtés matériels et spirituels de la nature humaine. Et, le seul terrain d’entente commun entre matière et esprit, c’est précisément que tous deux peuvent utiliser le nombre pour s’exprimer. L’un de manière quantitative comme somme d’unités. L’autre de manière plus qualitative, comme division d’une seule unité. Comme ce côté qualitatif des nombres est largement occulté dans notre éducation moderne, je vais brièvement le rappeler ici.
L’Ouroboros : fermé ou ouvert ?
Ainsi, au départ, il y a le nombre 0 qui, pour nos Anciens, symbolisait l’univers tout entier. Mais, dans un état non manifesté, c’est-à-dire latent, potentiel. Le symbole de l’Ouroboros, un serpent se mordant la queue, traduisait très bien cet état de fait. Toutefois, un autre nombre, le nombre 1, pouvait également jouer ce rôle. Mais, lui, décrivait un état manifesté, réel et visible de ce même univers. Ici, le serpent arrête de se mordre la queue. Il peut se déployer sous la forme d’une ondulation qui n’a ni début, ni fin. Bref, on dispose d’une unité, 1, et donc d’une essence pour toute chose à venir. La figure ci-dessous montre les diverses représentations, à travers les âges, de cet archétype du 0/1 indifférencié.

Discrimination et stabilité
Le nombre 2, était, pour sa part, le nombre de la discrimination. Autrement dit, une manifestation d’une polarité autorisant à différencier entre la tête et la queue du serpent cosmique. Cette polarité est, bien sûr, source d’instabilité, et donc de rythme, base de la vie. Parce que si je me situe à droite, la question se pose de savoir si cela ne serait pas mieux à gauche ? D’où l’insatisfaction, et donc le mouvement pour tenter de retrouver le calme initial. Ce qui est, bien sûr, impossible. Car, si deux apparaît, rien ne peut plus être comme avant. L’unité (1) s’est polarisée, et cette polarisation ne peut plus être annulée.
Toutefois, s’il est impossible de revenir au 1, on peut aller de l’avant à la recherche d’une stabilité dans le mouvement (2+1). On atteint ici le nombre 3, qui est le nombre par lequel s’exprime un monde vibratoire stabilisé. Mais, ici, un monde de nature spirituelle ou divine. Les Égyptiens l’ont gravé dans la pierre par la forme du triangle, tandis que les Grecs fondaient la philosophie avec la thèse, l’antithèse et la synthèse. De nos jours, la sagesse populaire retient le dicton : « Jamais 2 sans 3 ».
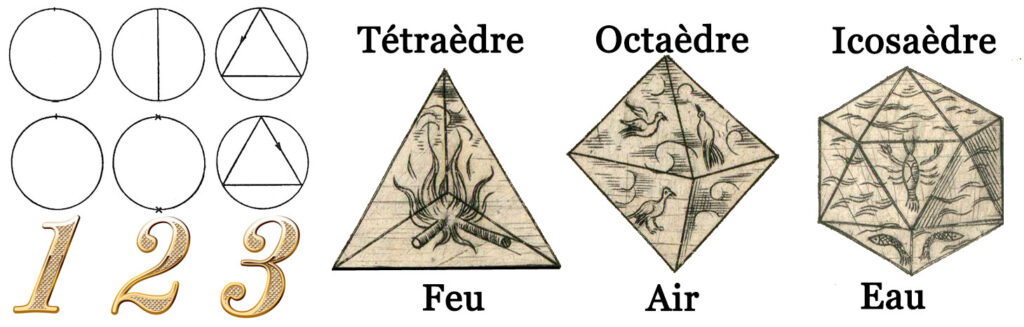
La figure ci-dessus montre les représentations géométriques associées aux chiffres 1 (cercle), 2 (diamètre d’un cercle) et 3 (triangle équilatéral). Le triangle est de fait le premier créateur de formes solides tridimensionnelles régulières comme le tétraèdre, l’octaèdre ou l’icosaèdre. Toutes ces formes 3D sont dotées d’une surface faite de triangles, mais également, d’un volume. Ceci permet de commencer à entrevoir des choses profondes appelées “éléments”. Toutefois, on notera qu’à ce stade, l’élément “Terre” est absent. Ceci signifie que l’on parle, à ce stade, d’un “feu divin”, d’un “air subtil” et d’une “eau spirituelle”.
La matière en relation avec l’esprit
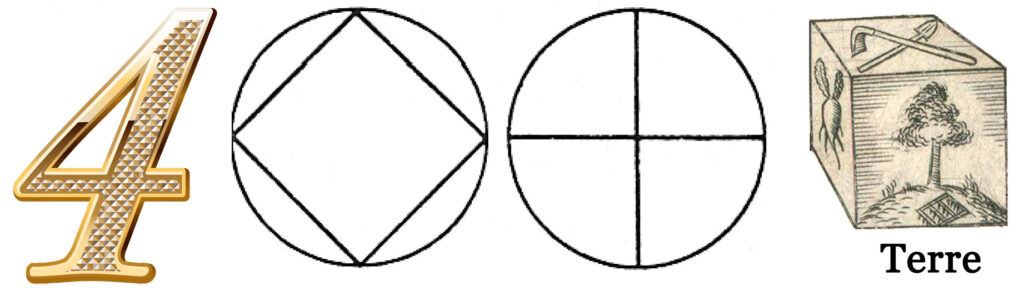
Le chiffre 3 peut être mis en relation avec la production d’un esprit stabilisé. Se pose alors la question de l’influence de cet esprit influence sur une chose extérieure à lui-même (3+1). D’où le chiffre 4, nombre de l’action ou du progrès, auquel on peut associer l’angle droit, le « gnomon » en grec. C’est-à-dire celui par lequel la connaissance arrive et où l’univers peut ainsi être créé. Le 4 est aussi le chiffre de l’incarnation terrestre de l’être humain. Il traduit l’activité de son esprit dans la matière.
D’où, bien sûr, les quatre éléments (Terre, Eau, Air et Feu) soumis à l’influence de trois principes (Sel, Soufre et Mercure). Principes que l’on peut considérer comme dérivant du feu divin, de l’air subtil et de l’eau spirituelle. Pour les solides tridimensionnels réguliers, on obtient ici un seul solide. Le cube, dès que trois carrés se rencontrent à angle droit. Mais, si quatre carrés essayent de se rencontrer en un même point, on n’a plus aucune profondeur. Il faut alors un nombre infini de carrés pour arriver à paver le plan, une surface dénuée de profondeur… La figure suivante illustre ces considérations. Elle montre également, qu’à ce stade, le carré génère la croix, forme géométrique duale du carré, mais ouverte.
Crise dans la matière
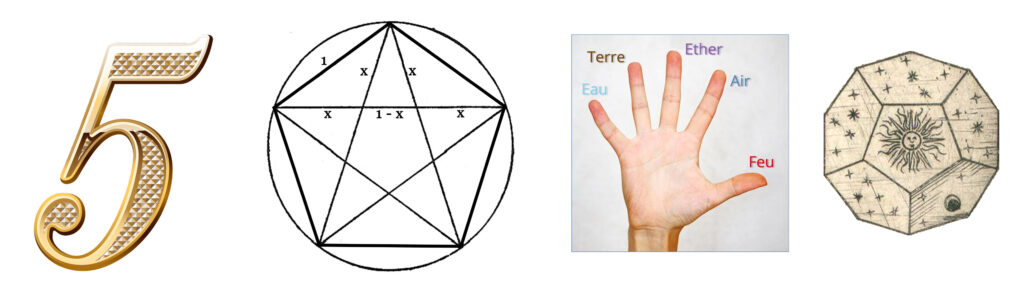
Que se passe-t-il si maintenant, j’applique mon action sur l’univers qui vient d’être créé (4+1). J’obtiens alors le nombre de la crise, soit le chiffre 5. Crise parce que, formellement, j’essaye par la même occasion de rendre instable (2) les choses ternaires intrinsèquement stables (5 = 3 + 2). Crise aussi de la conscience incarnée. Parce que la forme plane associée au 5, le pentagone, possède pour la première fois une forme étoilée duale, elle aussi fermée (le pentagramme étoilé).
Crise ensuite, par le fait que l’association de trois pentagones en un seul sommet, génère la dernière forme solide tridimensionnelle accessible à l’esprit : le dodécaèdre. Crise enfin, parce qu’avec quatre pentagones, je dépasse l’angle plein et ne suis même plus capable de paver le plan sans déborder. Mais, cette crise me permet également de quitter le monde des choses inertes pour entrer dans celui des formes vivantes qui expriment pleinement par le chiffre 5. Toute main ne possède-t-elle pas cinq doigts ?
Crise enfin, quand on réalise qu’il existe un cinquième élément, l’éther. Éther, qui nous introduit au fait que ce qui est matériel ne suffit pas à couvrir toute la réalité de l’univers. La figure suivante illustre ce concept de crise.
Beauté et Harmonie
Et, que génère la conscience incarnée lorsqu’elle agit sur le monde intelligible (5+1) ? L’instabilité liée au 2 réapparaît car (5 + 1 = 6 = 3×2). On obtient ainsi le nombre de l’accomplissement ou de la métamorphose (6). Le nombre de la beauté et de l’harmonie. De fait, la beauté peut se caractériser par le fait que l’intérieur d’un être est en harmonie avec son extérieur. Mathématiquement parlant, cela signifie que le nombre est égal à la somme de ses diviseurs, soit 6 = 3×2×1 = 3 + 2 + 1. Le nombre six était donc ce que les Grecs appelaient un « nombre accompli ». Comme « deux fois trois », six se présente sous la forme d’un hexagramme, soit deux triangles équilatéraux inversés l’un par rapport à l’autre. C’est le célèbre « sceau de Salomon ». Et, comme « trois fois deux », on trouve l’étoile formée de trois « bilatères ».
Mais, avec le nombre six, la force numérique capable de créer de la profondeur (solides 3D) commence à s’éteindre. On revient donc en surface dès que trois hexagones se rencontrent en un même point. C’est la structure en nid d’abeille ayant pour pavage dual le réseau dans lequel six triangles équilatéraux se rencontrent en un même point. C’est le prix à payer pour avoir la beauté. On peut aussi considérer que le créateur s’est uni à sa créature. La figure suivante résume graphiquement ce qui vient d’être dit.

Perfection
La beauté (6) est déjà quelque chose qui se situe au-delà de la matière inerte (4) ou vivante (5). Et, que se passe-t-il, si cette beauté souhaite passer au niveau de réalité supérieur (6+1) ? On obtient alors le nombre de la perfection, celui de l’univers dans sa totalité (7). Perfection qui se situe hors de portée de la règle et du compas. Et, qui peut aussi être vue comme la symbiose entre la stabilité (3) et l’action (4) puisque 7 = 4 + 3. Cette perfection se manifeste par l’heptagone régulier et les deux étoiles à sept branches associées. La première est obtenue en sautant un sommet dans l’heptagone. La seconde en sautant deux sommets. La figure suivante montre cette perfection à l’œuvre.

On y retrouve trois triangles isocèles qui sont les trois seules formes possibles de triangles isocèles permises par le chiffre sept. Comme le révèle la figure, il y a un éclair formé de quatre segments de même longueur x qui parcourt l’ensemble du triangle de sommets (3,1,3). On notera que le sept était en fait déjà présent comme cause agissante dans l’hexagramme. Considérez pour cela la triade inférieure et la triade supérieure situées l’une en face de l’autre (2×3). Puis, le cercle extérieur en tant qu’unité (1) planant au-dessus de l’hexagramme, soit 7 = 3 + 3 + 1. Et, remarquez qu’avec le six, on pouvait avoir un sol sous ses pieds (nid d’abeille). Avec le sept, le sol se dérobe. Et, on franchit donc un seuil d’ex-corporation, au-delà duquel on revient dans un monde spirituel.
L’épreuve de la mort initiatique
La perfection spatio-temporelle (7) ayant été atteinte, que se passe-t-il si j’essaye de passer au niveau supérieur (7 + 1) ? J’atteins alors le chiffre 8, le nombre de l’épreuve et de la mort initiatique. La chose parfaite meurt ainsi au monde extérieur (8), lorsqu’elle apparaît comme un octogone régulier (8 = 1×8) non cerclé. Mais, ce même huit peut aussi être vu comme l’entrelacement de deux carrés, puisque 8 = 2×4. On peut aussi juxtaposer les deux carrés, soit avec un côté commun, soit avec un sommet commun. On génère alors une forme géométrique proche du graphisme actuel pour ce chiffre.
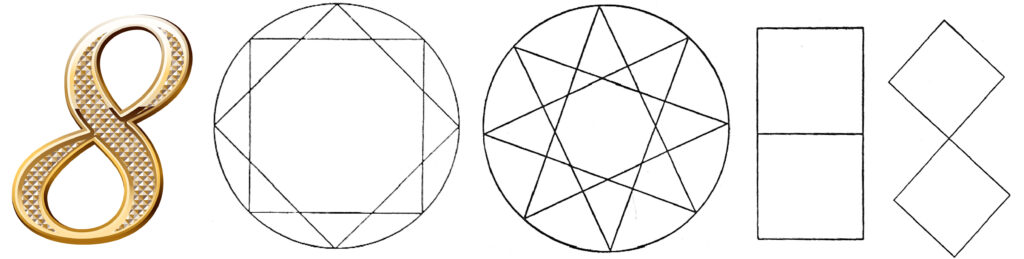
En revanche, l’indivisibilité de 8 par 3 s’exprime dans l’étoile à huit branches, comme le révèle la figure ci-dessus. La conservation de la perfection dans cette étape est assurée par le fait que 8 = 2×2×2 = 2³, et, que le chiffre 3 est garant de stabilité. Huit était, chez les Égyptiens, le chiffre de la divinité Thot, appelée aussi Hermès, chez les Grecs, puisque le huit apporte la possibilité de mourir au passé. Il s’agit ici, bien sûr, de guérir l’intérieur d’une chose, même si son extérieur reste parfait. Par conséquent, Thot était un dieu de l’Au-delà, qui enregistrait les jugements sur les âmes des morts. Parfois, c’était Thot lui-même qui pesait le cœur des morts par rapport à la plume de Maât dans la chambre des Deux Vérités.
Mais, comme l’hexagramme cerclé annonce le chiffre sept, le cerclage de l’étoile à huit branches annonce le chiffre neuf (9 = 8 + 1). Par conséquent, chaque fois que le huit se manifeste en concertation avec l’Ouroboros, quelque chose de neuf se prépare.
Nouveauté et renaissance
D’où l’idée de renaissance associée au chiffre 9 (9 = 8 + 1) et le nom « neuf » qui est particulièrement explicite. Pour construire un ennéagone, polygone régulier à neuf côtés, on part de l’hexagone cerclé de rayon r, auquel on rajoute ses trois diagonales (voir figure ci-dessous). On prolonge ensuite la diagonale vers la droite d’une longueur égale au rayon r du cercle.
Soit, maintenant, deux sommets A et B non adjacents de l’hexagone. Les deux droites partant de A et de B se rejoignent sur la diagonale horizontale et génèrent un triangle isocèle dont l’angle au sommet vaut 2×20° = 2π/9. La partie essentielle de cette figure (à droite) fait intervenir un triangle équilatéral, soit trois chiffres 3 (9 = 3 + 3 + 3). A gauche de ce triangle, on a un triangle isocèle (4, 1, 4, soit 4 + 1 + 4 = 9) en pointillé. A droite, on retrouve un autre triangle isocèle (2, 5, 2, soit 2 + 5 + 2 = 9), lui-même partageant une arête avec un troisième triangle isocèle (1, 7, 1, soit 1 + 7 + 1 = 9).
Les côtés de ces quatre triangles isocèles ont tous, par construction, la même longueur r. Ils génèrent un “éclair” depuis la base à gauche jusqu’à la pointe à droite. On constate alors que les quatre angles au sommet parcourent la série des nombres impairs : 1, 3, 5 et 7 inférieurs à 9. Tandis que leurs paires d’angles à la base parcourent la série des quatre nombres pairs inférieurs à 9 : 2, 4, 6, 8. Comme le révèle la figure, trois étoiles à neuf branches peuvent être dérivées de l’ennéagone régulier. Il suffit pour cela, de sauter un, deux ou trois sommets.
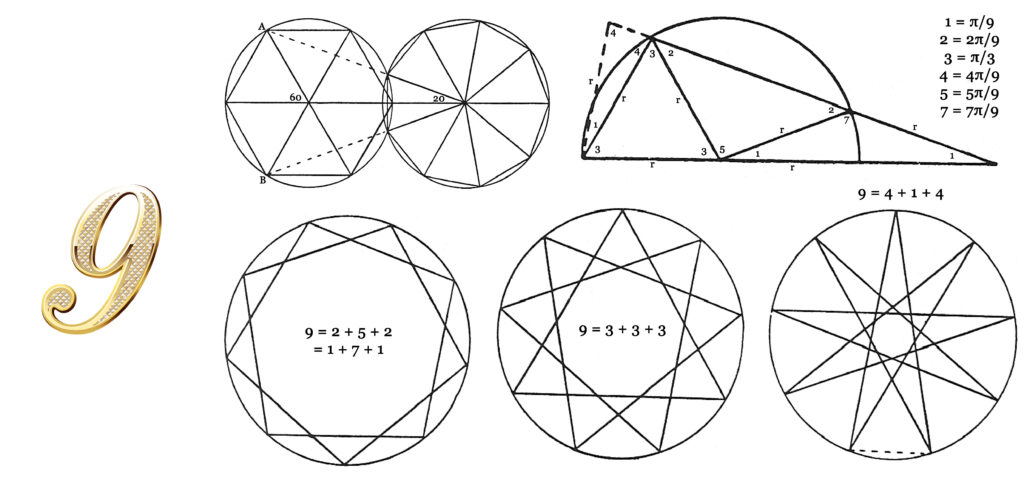
Naissance d’une nouvelle unité
Remarquons également que le chiffre 9 est marqué du signe de l’instabilité (2), par le simple fait que 9 = 3×3 = 3². Chez l’être humain, cela correspond, bien sûr, aux 9 mois de gestations après qu’une action masculine (4, le père) associée à une action féminine (4, la mère) génère un nouvel être (1, l’enfant), puisque 9 = 4 + 1 + 4. On est ainsi prêt à subir une évolution conduisant à une nouvelle entité sur un plan supérieur (10 = 9 + 1). La chenille s’est métamorphosée en papillon…
On remarquera que le 10, est lui-même instable parce que 10 = 5×2. Il ne contient donc pas le chiffre 3, gage de stabilité. Mais, on peut utiliser ici une procédure mathématique appelée, « racine numérique » qui consiste à additionner entre eux tous les chiffres constituant un nombre écrit en base 10. Ainsi, la racine numérique (RN) de 10 s’écrit 1 + 0 = 1, et l’on voit ainsi que dix est, en réalité, l’unité sous une nouvelle forme. L’essence de départ d’un nouveau cycle.
Retour à l’Ouroboros (nombre ou chiffre 0)
Il ne vous aura sûrement pas échappé qu’un polygone ou ses étoiles associées peuvent être représentés avec un cercle circonscrit ou pas. L’idée derrière la notion d’Ouroboros (cercle qui se referme sur lui-même), est qu’il ne connaît pas le repos. Il tourne indéfiniment sur lui-même. Quand il entoure un polygone ou une étoile, l’Ouroboros peut rapetisser en spirale jusqu’à en devenir le centre. Puis, comme point isolé au centre, il se déplace vers la périphérie. Ceci, afin de venir se fondre avec les (n-1) autres points du polygone. Ce faisant, le polygone à (n-1) côtés se métamorphose en polygone à n côtés. Ceci illustre la puissance de l’Ouroboros, dans sa capacité à transformer une chose ancienne en chose entièrement nouvelle. La figure suivante montre quatre polygones étoilés à cinq, six, sept et huit sommets.

Avez-vous là une représentation d’un pentagramme, d’un hexagramme, d’un heptagramme ou d’un octogramme ? Bien sûr que non. Le cercle circonscrit doit impérativement être pris en compter. Lorsque vous voyez de telles figures cerclées, songez qu’elles sont des graines pour représenter l’étoile ou le polygone d’ordre immédiatement supérieur. Ainsi, comme l’indique le chiffre au centre, le cercle autour du pentagramme indique qu’une crise (5) va aboutir à quelque chose de beau (6 = 5 + 1). De même, le cercle autour de l’hexagramme suggère que la perfection (7 = 6 + 1) est sur le point d’émerger de la beauté (6). Pour la même raison, le cercle qui entoure l’heptagone fait suspecter la mort (8 = 7 + 1) de quelque chose de parfait (7). Enfin, le cercle qui entoure l’octogone donne l’idée que ce qui est mort (8) va finalement pouvoir renaître (9 = 8 + 1).
Addition théosophique et Racine essentielle des nombres
En ayant traité les chiffres de 0 à 9, on a donc apparemment fini le travail. En vérité, pas réellement. Car, jusqu’à présent, les chiffres ont été formés par action de l’unité sur le chiffre précédent. Si cela permet de saisir leur individualité propre, cela ne permet en rien de saisir comment ils agissent en groupe. Pour cela, il nous faut introduire une seconde procédure mathématique appelée « addition théosophique » (AT). L’idée est de comprendre que lorsque je considère, par exemple, le chiffre 3, ce dernier n’arrive pas comme cela. Il contient aussi, en puissance, tous les chiffres qui le précèdent, à savoir 2, 1 et 0.
Une telle addition théosophique autorise alors d’accéder à la « racine essentielle » (RE = RN[AT]) des chiffres allant de 0 à 9. Puisque ces derniers ne peuvent pas avoir de racine numérique. Par exemple, on constate facilement que : AT(3) = 3 + 2 + 1 + 0 = 6. Ceci permet de comprendre que stabilité (3) et beauté (6) agissent de concert. Fort heureusement, il existe une formule permettant de calculer très rapidement l’addition théosophique de tout nombre n : AT(n) = n×(n + 1)/2. Ainsi, on a bien AT(3) = 3×4/2 = 6. On peut par conséquent dire que le chiffre 6 est la racine essentielle de 3. Ou bien, que le but de toute chose stable est de devenir belle.
Racines essentielles des nombres allant de zéro à neuf
On peut aussi, bien sûr, chercher la racine essentielle de 6. Ici, on dépasse le chiffre 10 puisque, AT(6) = 6×7/2 = 3×7 = 21. Toutefois, grâce à la racine numérique, on trouve que RE(6) = RN[AT(6)] = 2 + 1 = 3. On constate alors que la racine essentielle de 3 est 6. Sachant que la racine essentielle de 6 est 3. Cela signifie donc qu’une relation de réciprocité très forte unit ces deux chiffres. Considérons maintenant les chiffres restants :
AT(0) = 0×1/2 = 0 = RE(0).
AT(1) = 1×2/2 = 1×1 = 1 = RE(1).
AT(2) = 2×3/2 = 1×3 = 3 = RE(2).
AT(4) = 4×5/2 = 2×5 = 10, soit RE(4) = 1 + 0 = 1.
AT(5) = 5×6/2 = 5×3 = 15, soit RE(5) = 1 + 5 = 6.
AT(7) = 7×8/2 = 7×4 = 28, soit RE(7) = 2 + 8 = 10 = 1 + 0 = 1.
AT(8) = 8×9/2 = 4×9 = 36, soit RE(8) = 3 + 6 = 9.
AT(9) = 9×10/2 = 9×5 = 45, soit RE(7) = 4 + 5 = 9.
Cinq racines essentielles
On arrive ainsi à la conclusion qu’il n’existe que cinq racines essentielles : 0, 1, 3, 6 et 9. Ceci a l’avantage de mettre en valeur que les chiffres 1, 4 et 7 partagent la même racine essentielle (1) qui est l’unité elle-même. Cela nous indique que s’il y a un commencement (1), il doit nécessairement y avoir un progrès (4) devant aboutir à un terme parfait (7). Ce triplet (1, 4, 7) acquiert ici une universalité pour tout ce qui évolue dans l’univers. Car, on peut dire que l’unité (1) se manifeste par 4 et 4 se réalise à la perfection par 7.
Il reste alors 3 doublets (2,6) ; (3,5) et (8,9) associés à un triplet de racines essentielles (3, 6, 9). Le doublet (2,6) signifie discriminer pour atteindre la beauté. Le doublet (3,5) signifie que toute stabilité conduit tôt ou tard à une crise. Enfin, le doublet (8,9) signifie qu’après toute épreuve pouvant conduire à une mort, vient une renaissance, sous la forme de quelque chose de neuf.
L’Amour
On comprend ainsi comment, il est possible de parler intelligemment de choses sur un plan uniquement qualitatif. La nature quantitative (compter), passe ici au second plan. Pour cela, nous nous sommes appuyés sur un mélange de sagesse antique et de science mathématique. Bref, on a simultanément une approche artistique qualitative couplée à une approche scientifique, plutôt quantitative. D’où, finalement, une possibilité de définir ce que l’on appelle l’amour :
Au tout début, amour de ce qui est vide (0), puisque ce vide contient tout (1, 10).
Puis, amour qui incite à toujours progresser (4), pour atteindre une perfection (7).
Il y a également l’amour de la stabilité (3), sachant qu’il y aura crise (5).
Mais, encore, amour de la beauté (6), sachant qu’il y aura instabilité (2).
Enfin, amour de la nouveauté comme aptitude à renaître guéri (9) après toute épreuve (8).
Peur et sérénité
On comprend aussi ici pour quelles raisons les chiffres (2, 5 et 8) sont généralement associés à la notion de « peur ». Les autres (3, 6 et 9) étant, au contraire, plutôt associés à la notion de « sérénité ». Tout cela démontre comment nos anciens étaient passés maîtres dans l’art de manier les chiffres, sur un plan qualitatif. L’image associée à cette chronique résume ce que nous venons de voir. Vous pouvez d’ores et déjà méditer dessus pour analyser ce qui se passe actuellement dans le monde. Les clés qu’elle propose sont extraordinairement puissantes. Elles devraient vous permettre de vous y retrouver et surtout de ne pas paniquer.
Nombres inaccessibles
Pour conclure, je souhaiterais vous dire quelques mots sur la notion d’inaccessibilité. Là, plus question de sagesse antique. On va plutôt utiliser le raisonnement mathématique pur et dur. Ainsi, en arithmétique, un nombre (m) est dit inaccessible si chaque somme ou produit de moins de m nombres strictement inférieurs à (m) est strictement inférieure à lui-même. Selon ce critère, tous les entiers naturels supérieurs ou égaux à 3 sont accessibles…
Les seules exceptions sont les nombres 0, 1 et 2. Toutefois, comme 0⁰ = 1, le nombre 1 est accessible à partir du nombre 0 qui lui est strictement inférieur. Les nombres 0 et 2 sont donc les seuls nombres finis fortement inaccessibles par l’addition, la multiplication ou l’exponentiation. Ceci nous sera utile pour la prochaine chronique. En attendant, bonne méditation. Surtout si vous méditez en écoutant le tout dernier album de Tommi Jack’s qui est au diapason de l’eau (429,62 Hz) : « La de l’Eau ».
Références
[1] L.-C. de Saint-Martin, « Les Nombres », première édition authentique par Robert Amadou avec dessins de l’auteur, Documents martinistes, Cariscript, Paris, 1983.
[2] Ernst Bindel, « Les Nombres et leurs fondements spirituels », Éditions Anthroposophiques Romandes, Genève, 1992.
[3] François-Xavier Chaboche, « Vie et Mystère des Nombres », Albin Michel, 1976 ; Éditions de Compostelle, 1989.



Leave a Reply