Volume, masse ou nombre de moles ?

Il existe trois manières principales d’exprimer la quantité de matière. On peut ainsi mesurer des volumes, des masses ou des nombres de moles. La question se pose donc de savoir s’il n’y a pas une mesure qui est plus fondamentale que les autres. La réponse à cette question dépend du but que l’on recherche.

Si l’on s’intéresse à l’aspect expérimental et pratique des choses, il est évident que les unités de volume et de masse sont de loin les mieux adaptées. En effet, dans tout laboratoire scientifique qui se respecte, on trouve des fioles, des pipettes et des seringues pour manipuler des liquides. Et, il y a aussi bien sûr des balances pour régler les proportions des matières solides.

Convertir les volumes en masses

Travailler en moles semble donc bien abstrait lorsque l’on s’intéresse uniquement à l’aspect pratique des choses. Une personne qui a pris l’habitude de raisonner en masse ou en volume ne peut, en effet, que constater des phénomènes. Ici, impossible de comprendre ce qui se passe. Il est d’autre part clair que l’unité de masse est de loin préférable à l’unité de volume. En effet, suite aux phénomènes de dilatation thermique et de compressibilité isotherme, les volumes peuvent varier pour une même masse dès que la température ou la pression change.

Dès lors, raisonner en volume suppose que l’on a pris le soin de s’assurer que température et pression restent rigoureusement constants durant toute la durée de l’expérience. Ceci complique considérablement la pratique expérimentale de laboratoire. La masse est donc une quantité qui reste toujours la même quelles que soient les conditions de température et de pression. Il est donc plus fiable de raisonner sur la masse que sur le volume. La toute première étape de compréhension du mode de fonctionnement de la nature sera donc une conversion des volumes en masses. On utilise pour cela la notion de densité ou de masse volumique.

Conversion des masses en nombre de moles

Ayant converti tous les volumes en masses, il reste un problème. Celui du passage de l’aspect macroscopique des choses (masses) à l’aspect atomique ou moléculaire (moles). Car, dans tout processus physique, chimique ou biologique il y a des objets en mouvements qui peuvent se rencontrer à tout moment de leur existence. L’un des progrès décisif du XIXᵉ siècle fut ainsi d’arriver à comprendre ce qui se passe à une échelle de taille suffisamment petite, voisine du milliardième de mètre.

Ici, la matière ne peut plus être divisée en partie équivalentes du point de vue de la masse. À cette échelle extraordinairement petite qui échappe à nos sens, nous entrons dans le royaume des molécules. Toutes ces molécules sont constituées à partir d’une centaine de briques fondamentales appelées “atomes”.

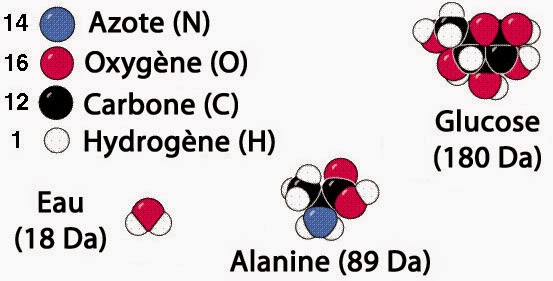
Raisonner en masse, n’est ici plus d’aucune utilité. Pour avoir une bonne compréhension des raisons qui poussent la matière à se déplacer ou à se transformer, il faut impérativement convertir toutes les masses en moles. Rester désespérément accroché aux masses, signifie que l’on nie l’existence même des atomes. Ceux qui se sont aventurés dans cette voie au XIXᵉ siècle, les fameux “équivalentistes”, l’ont amèrement regretté par la suite.

Atomes et molécules

En effet, sans la notion d’atomes, il est très difficile de progresser dans la compréhension fine du comportement de la matière. D’un point de vue pratique le passage de la masse au nombre de moles nécessite de connaître la masse molaire. Cette dernière s’exprime au moyen d’une unité appelée “Dalton” (symbole Da ou u). Cette unité indique la masse (en grammes) correspondant à une mole de matière. C’est-à-dire à un ensemble de 6,02214076×10²³ entités atomiques ou moléculaires (nombre d’Avogadro).

De manière équivalente, le millième de l’inverse de ce nombre d’Avogadro, donne le facteur de conversion entre le dalton et l’unité SI de masse (le kilogramme), soit: 1 Da = 1,66053906660(50)×10⁻²⁷ kg = 1 u.