Épisode 26 Covid-19, juin 2020
Fréquence et probabilité
On ne doit jamais confondre, fréquence f = m/n et probabilité p = M/N. Les définitions des paramètres m, n, M et N ont été donnés dans la précédente chronique. Pour obtenir une fréquence f il est impératif de pouvoir répéter une expérience de multiples fois. La fréquence constitue une propriété factuelle du monde réel, que l’on peut mesurer ou estimer. Elle ne nous renseigne sur une probabilité que si le nombre d’expériences tend vers l’infini. Or, ce qui intéresse le péquin lambda ce n’est pas le monde réel, mais le monde futur. S’intéresser au monde réel est l’apanage des comptables qui peuvent vous abreuver de chiffres jusqu’à en avoir la nausée. Le point de presse quotidien de Mr Salomon vous a montré un comptable à l’œuvre. Qu’en avez-vous déduit pour votre vie quotidienne ? Absolument rien. Sinon, peut-être, un sentiment de tristesse et de lassitude, au fil des minutes.
Ceci m’amène au gros bout du problème. Celui qui seul vaut la peine que l’on s’intéresse aux chiffres. Je veux en effet anticiper le futur en fonction de ce que je sais du présent. Là, on passe d’un exercice purement comptable à un exercice d’ordre scientifique. Si je parle de gros bout, c’est bien sûr parce qu’il ne suffit pas d’estimer une fréquence, mais bien une probabilité. Comme il s’agit ici de raisonner et non plus de calculer, beaucoup jettent l’éponge. On peut, bien sûr, toujours se fier à l’intuition en ne faisant aucun calcul. Toutefois, dans notre monde hyper technique et spécialisé cela ne suffit pas. Car la subjectivité de l’individu peut interférer avec son intuition, pour le meilleur comme pour le pire. L’idée est de rester objectif et neutre, tout en inférant le futur à partir de la seule donnée du passé et du présent.
L’abbé et le savant
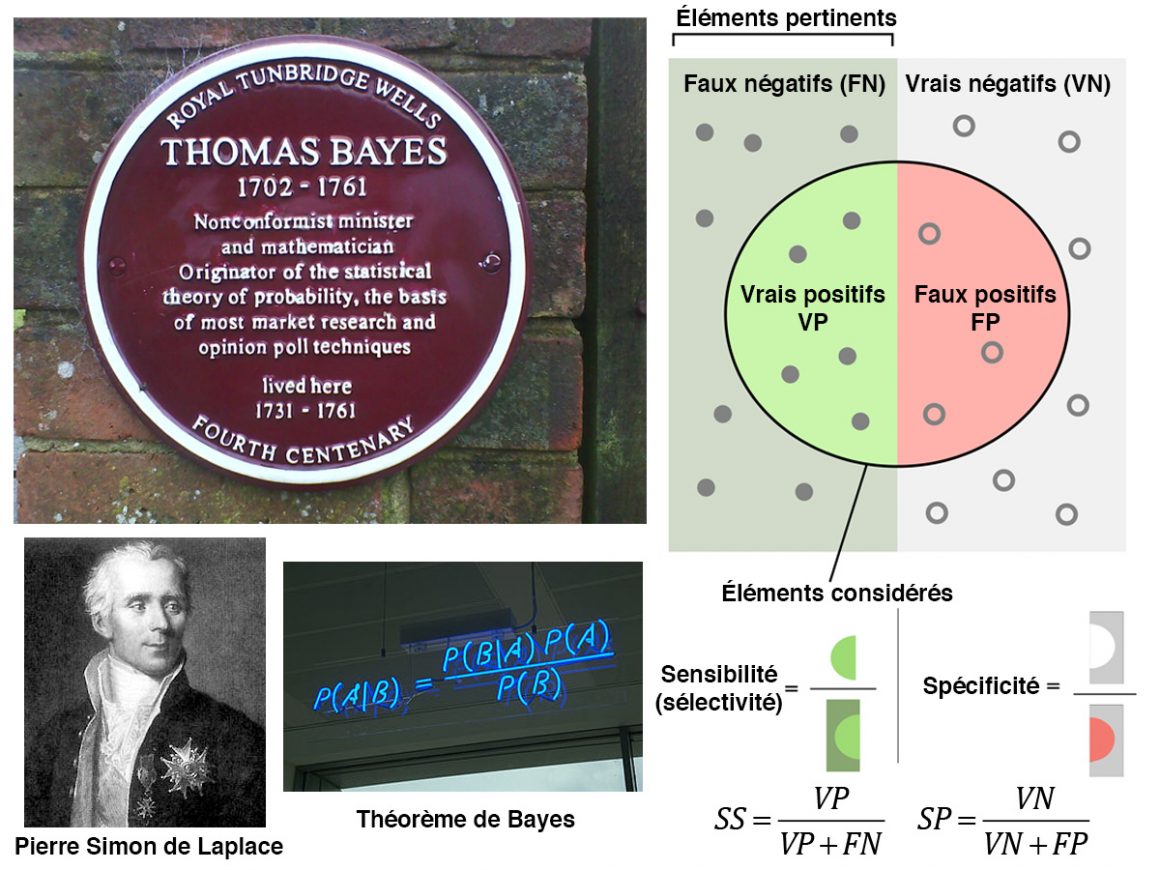
C’est l’ecclésiastique britannique Thomas Bayes (1702-1761) qui nous a légué la recette infaillible pour rester objectif. Il a en effet compris que la probabilité inverse est beaucoup importante que la probabilité directe. Personne ne fit bien sûr attention à son théorème. Il sombra donc bien vite dans l’oubli. En 1774, le physicien Pierre Simon de Laplace (1749-1827) redécouvre le théorème de Bayes. Laplace l’appliqua ainsi à des problèmes aussi variés que l’astronomie, la géodésie, la météorologie, la démographie voire la jurisprudence. C’est ce théorème de Bayes qui permet de sortir d’un simple exercice de comptabilité.
C’est aussi à ce niveau que se produit le grand schisme entre deux familles de statisticiens. Il y a en effet ceux qui cherchent à estimer la probabilité à partir de la fréquence en se basant sur la loi des grands nombres. Il y a aussi ceux, les Bayésiens, qui cherchent à estimer la probabilité par inférence. Ils utilisent pour cela de manière extensive la règle de Bayes. Autant l’avouer tout de suite, les deux communautés se haïssent. Il s’agit ici d’une haine archaïque bien profonde et non d’un simple différend technique. Car l’emploi de la loi des grands nombres ne donne accès qu’au passé et au présent. Impossible d’inférer, dans ces conditions, quelque chose sur le futur. Pour imaginer le futur, il est d’impératif d’utiliser la règle de Bayes.
Les règles de Laplace
Le grand mathématicien Laplace a en effet formalisé les idées de Bernoulli sur le produit et la somme des probabilités. Il faut pour cela considérer trois types de probabilités :
- Il y a la probabilité p(A et B) que les propositions A et B soient vraies simultanément.
- On trouve aussi la probabilité p(non-A) = 1 – p(A) que la proposition A soit fausse.
- Enfin, il y a la probabilité conditionnelle p(A si B) que la proposition A soit vraie sous l’hypothèse que B est vraie.
Supposons maintenant que A représente une hypothèse ou une théorie plausible dont on souhaite vérifier la validité. B va représenter une nouvelle donnée en provenance de l’observation (présent). Enfin C représentera l’information donnée a priori. C résume donc la totalité de ce que nous connaissons sur A avant l’acquisition de la donnée B (passé).
Les règles de maniement des probabilités, le petit bout, s’écrivent alors formellement :
- p[A et (B si C)] = p[(A si B) et C]×p(B si C)
- p[A si B] + p[(non-A) si B] = 1
Le théorème de Bayes
Bon, je sais, pour certains d’entre vous c’est déjà un gros bout. Toutefois, rien dans la vie ne s’obtient sans un effort minimal. Car, il y a un bout encore plus gros à avaler. Le mot clé « si » montre que l’on a bien affaire à des probabilités conditionnelles. On fait ici uniquement référence au passé et au présent. Le futur s’introduit dans le raisonnement en remarquant que (A et B) et (B et A) correspondent à la même proposition. La cohérence impose donc que l’on puisse échanger A et B dans (1). On arrive ainsi au théorème de Bayes, le gros bout :
p[A si (B et C]×p[B si C] = p[A si C]×p[B si (A et C)]
Il est crucial de comprendre ce qui se cache derrière sous cette dernière forme. Elle nous donne en fait une représentation mathématique de la manière dont l’être humain fonctionne. Ainsi, p(A si C) est la probabilité a priori ou antérieure que A soit vraie lorsque nous ne disposons que de l’évidence C. L’expression p[A si (B et C)] est la probabilité a posteriori ou postérieure, réajustée lorsque nous avons acquis une nouvelle information B. L’intérêt du théorème de Bayes est qu’il peut être enchaîné chaque fois que de nouvelles informations B1, B2… sont acquises. La probabilité postérieure de chaque expérience devient alors la probabilité antérieure de l’expérience suivante. C’est ainsi qu’il est possible d’arriver jusqu’à d’éventuelles quasi-certitudes.
Savoir manier l’ignorance
Malheureusement, le travail de Laplace sombra lui aussi bien vite dans l’oubli. L’astronome Sir Harold Jeffreys (1891-1989) le redécouvrira dans les années 1930. Surtout Jeffreys indique comment choisir l’espace des hypothèses selon une connaissance a priori du système. L’idée de base est d’attribuer la même probabilité à deux problèmes où l’on dispose du même état de connaissance. Pour les matheux de service, il s’agit ici d’un principe général d’invariance dans un groupe afin de représenter notre état d’ignorance. Notons que le fait d’assigner des probabilités égales à deux évènements ne signifie en rien que ces derniers se manifesteront avec une fréquence égale lors de toute expérience aléatoire. Il s’agit simplement de formaliser mathématiquement le fait que notre ignorance des probabilités respectives est totale.
En effet, il peut très bien arriver que les évènements en question ne puisse pas être répétés. La probabilité devient donc ici un concept abstrait. C’est une quantité assignée théoriquement afin de représenter un état de connaissance. L’intérêt est que l’on peut aussi la calculer au moyen de probabilités préalablement assignées au moyen du théorème de Bayes. Le théorème de Bayes est donc un contexte purement mathématique qui permet de pouvoir inférer des conclusions les plus sûres possibles à partir d’une information incomplète. Il évite de commettre l’erreur d’identifier probabilité et fréquence. Après avoir avalé, le gros bout, que faire ? Eh bien constater, par exemple, comment on vous manipule avec cette histoire de tests pour détecter le COVID-19. Car tout test est conçu selon deux critères :
Sensibilité et spécificité d’un test
Sa sensibilité SS = p(positif si infecté), qui mesure le taux de personnes infectées avérées positives au test.
Sa spécificité SP = p(négatif si non-infecté), qui mesure le taux de personnes non infectées avérées négatives au test.
Entre aussi en ligne de compte la prévalence de la maladie, c’est-à-dire la probabilité d’être infecté, P(I). La question à mille francs est bien sûr de connaître la probabilité p(infecté si positif). Sans le théorème de Bayes on va commettre l’erreur d’écrire que p(infecté si positif) = p(positif si infecté) = SS. Par contre si l’on applique le théorème de Bayes, on écrira que :
p(positif)×p(infecté si positif) = p(infecté)×p(positif si infecté) = p(I)×SS
p(négatif)×p(non-infecté si négatif) = p(non-infecté)×p(négatif si non-infecté) = p(I)×SP
La clé est donc de bien penser à pondérer chaque probabilité conditionnelle par la probabilité de l’événement qui vient de se produire. C’est-à-dire qu’il ne suffit pas d’être positif au test. Il faut aussi connaître la probabilité d’avoir un test positif qui concerne, elle, toute la population testée. Elle s’obtient en additionnant le produit des fréquences par les probabilités conditionnelles correspondantes. Bien évidemment, soit il y a infection, soit il y a non-infection. Donc p(non-infecté) = 1 – p(I). De même, en cas de non-infection, le test pourra être aussi bien positif que négatif. Donc p(positif si non-infecté) = 1 – (négatif si non-infecté) = 1 – SP et p(négatif si infecté) = 1 – (positif si infecté) =1 – SS. D’où les probabilités d’être positif ou négatif à un test de sensibilité SS et de spécificité SP pour une prévalence P(I) :
p(positif) = p(infecté)×p(positif si infecté) + p(non-infecté)×p(positif si non-infecté)= p(I)×SS + [1 – p(I)]×(1 – SP)
p(négatif) = p(non-infecté)×p(négatif si non-infecté) + p(infecté)×p(négatif si infecté) = [1 – p(I)]×SP + p(I)×(1 – SS)
Infecté ou non-infecté ?
D’où le moyen d’évaluer ses chances d’infection en cas de test positif ou négatif :
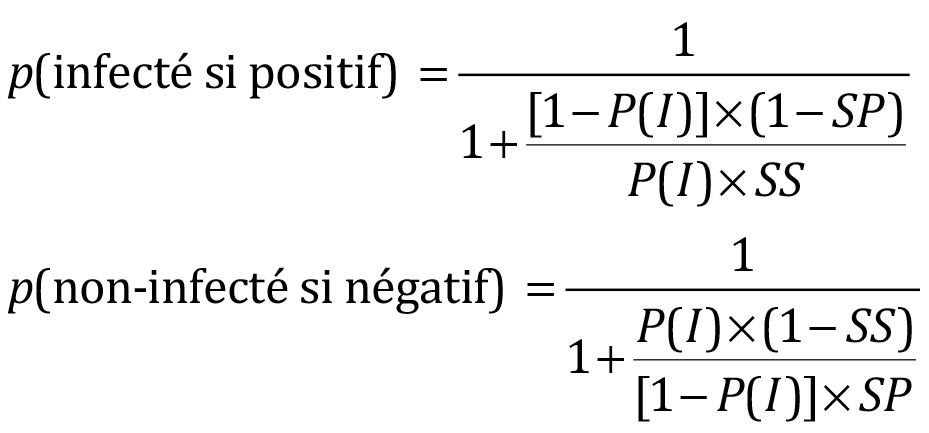
Soit donc un test rt-PCR positif au COVID19 de sélectivité SS = 0,55, de spécificité SP = 0,75 % pour un taux de prévalence P(I) = 0,0238 %. L’application du théorème de Bayes conduit donc à p(infecté si positif) = 0,051. Si le test s’avère positif, Il n’y a donc que 5 chances (objectives) sur 100 d’être réellement infecté. La deuxième formule conduit pour sa part à p(non-infecté si négatif) = 0,986. Si le test s’avère négatif, il n’y a donc que 1 chance objective sur 100 d’être infecté.
Pour les non-matheux
Si les mathématiques vous rebutent, vous pouvez aussi raisonner ainsi. Sur 10000 personnes 238 seront infectées puisque p(I) = 2,38 %. Sur ces 238 personnes infectées, 238×0,55 ≈ 131 auront un test positif puisque la sélectivité n’est que 0,55 (0,45 de faux négatifs). Pour les 1000 – 238 = 9762 autres personnes qui ne sont pas infectées, environ 9762×(1 – 0,75) = 2440 auront un test positif puisque la spécificité du test n’est que 0,75. Donc, sur un total de 131 + 2440 = 2571 personnes positives, 131 ayant été réellement infectées auront été détectées. La probabilité d’être infecté en cas de test rt-PCR positif au COVID-19 est donc 131/2571 = 0,051. Soit le pourcentage précédemment trouvé par la première formule.
De même, Sur les 9762 personnes non-infectées, 9762×0,75 ≈ 7322 auront un test négatif. Pour les 238 personnes restantes infectées, environ 238×(1 – 0,55) = 107 auront un test négatif (0,45 % de faux positifs). Donc, sur un total de 107 + 7322 = 7429 personnes négatives, 7322 n’ayant pas été infectées auront été détectées. La probabilité de ne pas être infecté en case de test rt-PCR négatif au COVID-19 est donc 7322/7429 = 0,986. C’est bien le pourcentage que l’on obtient avec la deuxième formule.
COVID-19, Mammographie et VIH
Pour que le test (tel qu’il est) soit vraiment indicatif, il faudrait que le virus soit très contagieux. Par exemple avec P(I) = 0,5, on aurait p(infecté si positif) = 0,69 contre p(non-infecté si négatif) = 0,63. Si on détecte bien mieux les cas positifs, on est en revanche beaucoup moins sûr pour les cas négatifs. On peut aussi changer de test. Par exemple, les tests sérologiques où l’on recherche la présence d’un antigène sont peu sensibles (SS = 0,602) mais très spécifiques (SP = 0,992). Avec P(I) = 0,0238, on aura p(infecté si positif) = 0,647 et p(non-infecté si négatif) = 0,991.
Ceci montre que si l’on peut se fier à un test négatif, le fait d’être positif ne signifie rien du tout, sauf si la maladie est très fréquente. Notez bien que ceci est vrai pour tous les tests de santé quels qu’ils soient. Par exemple pour les mammographies, on a SS = 0,9 et SP = 0,93 pour P(cancer du sein) = 0,008. D’où un risque de cancer de seulement 9 % en cas de mammographie positive. Donc, mesdames, avant de vous faire enlever un sein, demandez simplement une autre analyse plus fiable.
De même, le test ELISA pour détecter le VIH est extrêmement sensible SS = (0,999) et abominablement spécifique (SP = 0,9999). Pour autant, le SIDA ne touche que 0,01 % de la population, soit p(I) = 0,0001. Je fais un test ELISA qui me déclare séropositif. Que faire ? Eh bien avant de m’affoler, j’applique le théorème de Bayes. Soit ici p(infecté si positif) ≈ 0,5. Chic ! Car après tout j’ai encore une chance sur deux de ne pas avoir le SIDA…
La grande illusion
La conclusion est qu’un test n’a de valeur que si le résultat qu’il produit est négatif. En cas de test positif, tout va dépendre des valeurs relatives de la prévalence de la maladie, de la sensibilité et de la spécificité du test. Donc, lorsqu’on affirme que l’on va utiliser des tests pour savoir s’il faut confiner les personnes infectées, on peut rigoler. Car les tests ne sont fiables qu’en cas de réponse négative. On est donc, dans ce cas, pas plus avancé avant et après le test. Si la réponse est par contre positive, il y a une suspicion. Pour être sûr, il est bon de s’enquérir de la fiabilité du test. Ou mieux : faire un autre test.
Par contre, une chose est certaine. C’est que l’on a enrichi considérablement les entreprises qui commercialisent lesdits tests. Donc les Chinois entre autres. Tiens, tiens, tiens… Comme le monde est petit. J’arrête donc là car après on quitte la science pour le commerce.
Par Marc HENRY


Leave a Reply