Tableau périodique des éléments

Classer les atomes

La construction du tableau périodique des éléments fut l’œuvre du chimiste russe Dimitri Ivanovich Mendeleev (1834-1907). Ainsi, les atomes, par leurs combinaisons diverses et variées génèrent tout le monde matériel qui nous entoure. Un des grands succès de la physique quantique est d’avoir pu, en partie seulement, justifier un tel classement atomique. Car, ce tableau postule que les éléments chimiques trouvés dans la nature forment des périodes. Il est bon toutefois de souligner que la physique quantique n’est toujours pas capable, même aujourd’hui d’expliquer tous les détails du tableau périodique.

Car, comme on le voit rarement écrit, l’expérience reste nécessaire pour dériver la forme générale du tableau. Autrement dit, la chimie ne peut pas être réduite à une simple sous-discipline de la physique. Les personnes intéressées pourront consulter la page suivante pour plus de détails. Ici, nous nous intéressons à la genèse du tableau périodique dans le cadre de la théorie des quanta (1899-1926). Cette théorie est maintenant abandonnée. Toutefois, elle a permis l’éclosion de la physique quantique telle que nous la connaissons aujourd’hui.

Construire les atomes

En 1913, Niels Bohr donne une expression théorique claire et exacte de la constante empirique de Rydberg. Toutefois, Niels Bohr avait aussi comme ambition d’interpréter tout le tableau périodique au moyen de configurations électroniques. En effet, Bohr assignait à chaque élément du tableau périodique, une configuration électronique. Il utilisait pour cela un nombre quantique principal, c’est-à-dire un entier n strictement positif n, dérivé de sa théorie de l’atome d’hydrogène. Bohr appelait cela le “aufbauprinzip“.

Il s’agissait d’un principe de construction des atomes correspondant à des éléments successifs dans le tableau périodique en ajoutant un électron à l’atome précédent. L’électron était toujours ajouté dans la couche la plus externe. Ceci jusqu’à atteindre un nombre maximal égal à 2·n², où n était le nombre quantique de la couche en cours de remplissage. Dès qu’une couche de valence d’indice n était remplie, elle devenait une couche interne dite de cœur. Il apparaissait alors une nouvelle couche de valence d’indice (n+1) pour continuer le remplissage.

Résultat

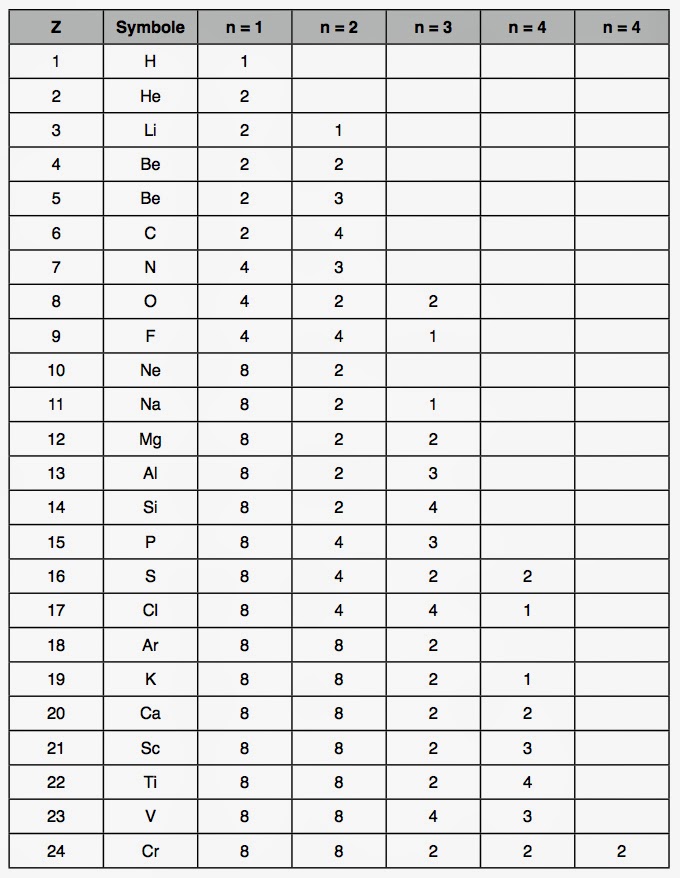
De plus, la population de ces couches de valence était déduite de la connaissance des valences chimiques des éléments. On obtenait ainsi le tableau représenté plus haut.

On constate que Bohr ne dérive pas de manière rigoureuse son modèle atomique de la théorie quantique. Pour faire son remplissage, il utilisait plutôt son intuition couplée aux données spectroscopiques et chimiques. On le voit très bien au niveau des éléments azote, phosphore et arsenic. En effet, pour justifier la valence 3 observée chimiquement, il y a des sauts abrupts dans les couches de cœur. De plus, rien ne justifiait sur le plan théorique que la capacité maximale d’une couche était de 2·n² électrons.

Atomes relativistes

Toutefois, le remplissage de Bohr avait l’avantage de suggérer l’idée que des éléments ayant des propriétés chimiques voisines (Li, Na) ou (Be, Mg) provenait du fait que leurs couches de valence externe étaient similaires. C’est alors qu’Arnold Sommerfeld proposa un traitement relativiste de l’atome d’hydrogène. Bohr modifia donc en conséquence son système en 1922 et 1923. En effet, Bohr supposait que le mouvement des électrons autour du noyau pouvait être assimilé à des cercles ou orbites indexés par son nombre quantique principal n. Ce nombre avait pour fonction principale de quantifier le mouvement radial de l’électron.

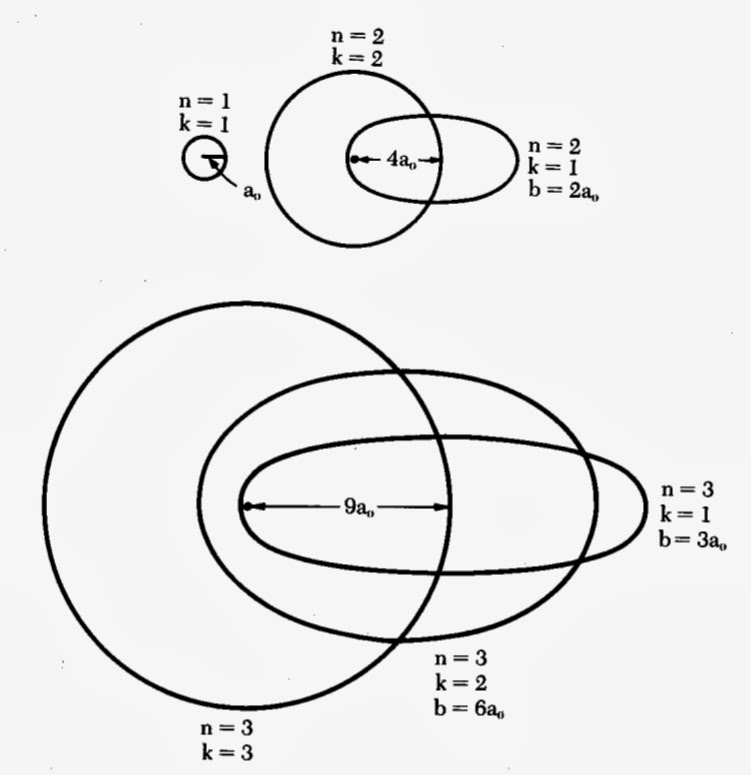
Sommerfeld, lui réalisa qu’il s’agissait plutôt d’ellipses. Ceci impliquait l’existence d’un second nombre quantique k, dit azimutal. Son rôle était de quantifier le mouvement orbital de l’électron dans le plan de l’ellipse. Grâce à un traitement relativiste du problème, il montra que l’énergie était donc quantifiée à l’aide d’une paire de nombres (n, k) selon l’expression :

E(n,k) = -Z^{2}\cdot R\cdot hc\left \lfloor \frac{1}{n^{2}} + \frac{\alpha ^{2}\cdot Z^{2}}{n^{4}}\left (\frac{n}{k} - \frac{3}{4} \right ) \right \rfloor

Ceci permettait d’expliquer la structure fine du spectre d’émission de l’atome d’hydrogène puisque tout niveau d’indice n était un multiplet indexé par l’indice k. Les orbites circulaires de Bohr correspondaient au cas où k = n. Pour k ≠ n, le rapport des demi-axes de l’ellipse valait b/a = k/n.