Énergie interne U et enthalpie H

Le premier principe de la thermodynamique peut s’écrire sous deux formes entièrement équivalentes. Si l’on travaille à chaleur Q et volume constant V, on a :

dU = dQ – P·dV

Par contre, si l’on travaille ou à chaleur et pression constante, on aura plutôt :

dH = dQ + V·dP

Ces deux fonctions d’états U (énergie interne) et H (enthalpie) sont reliées l’une à l’autre par une transformation de Legendre H = U + p·V. En fait, ces expressions ne sont valables en toute rigueur que pour les matières gazeuses. Car, dans un tel état les énergies potentielles sont négligeables devant l’énergie cinétique de mouvement. Dans le cas des solides, l’énergie interne U peut s’exprimer au moyen d’une certain nombre de paires de variables conjuguées selon :

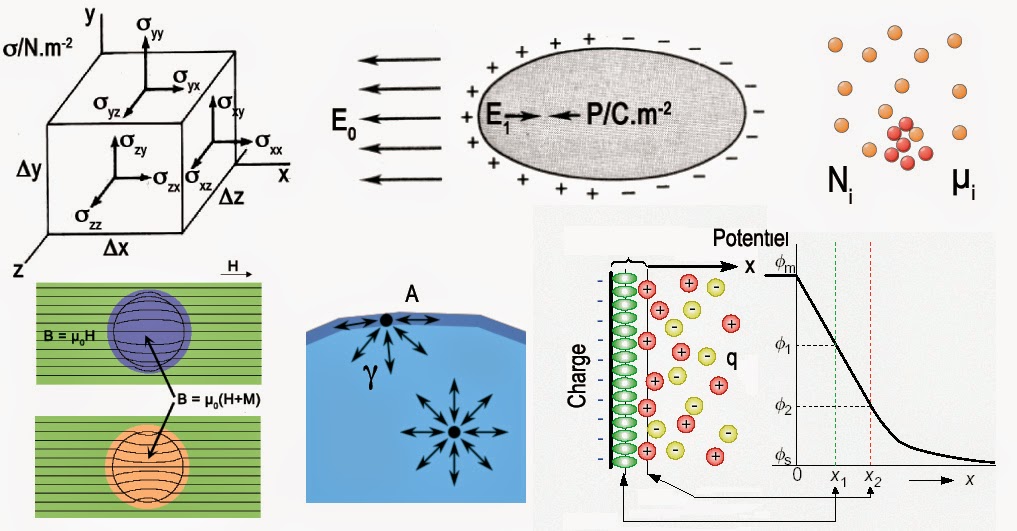
dU = dQ + \sum\limits_{i = 1}^3 {\sum\limits_{j = 1}^3 {{\sigma _{ij}}d(V{\eta _{ij}})} }  - \sum\limits_{i = 1}^3 {{E_i}d(V{P_i})}  - \sum\limits_{i = 1}^3 {{B_i}d(V{M_i})}  + \sum\limits_{i = 1}^n {{\mu _i}d{N_i}}  + \phi dq + \gamma dA

Énergies potentielles

Cette expression s’applique à tout solide. Elle prend en compte, toutes les formes d’énergie potentielles. Ainsi, le premier terme fait intervenir le tenseur de déformation en volume V·η_ij qui s’exprime en unité m³. Sa variable conjuguée  est le tenseur de contraintes σ_ij qui s’exprime en N·m^-2. Le second terme traduit la polarisation électrique de la matière sous l’effet d’un champ électrique E_i dont l’unité est le V·m^-1. Sa variable conjuguée est le moment dipolaire volumique V·P_i qui s’exprime en C·m. Il y a aussi la magnétisation sous en la présence d’une densité de flux magnétique B_i mesurée en teslas (T). La variable conjuguée est dans ce cas, le moment magnétique en volume V·M_i qui s’exprime en A·m².

Le terme suivant prend compte toute transformation chimique. On y retrouve la variable conjuguée du potentiel chimique µ_i qui s’exprime en J·mo^l-1 ) qui est le nombre de moles N_i. Les termes suivants s’appliquent à la surface du solide et non à son volume. Il y a donc la variable conjuguée du potentiel électrique φ(V) qui est la charge électrique interfaciale q(C). Enfin si A est l’aire du système, sa variable conjuguée est l’énergie interfaciale γ qui s’exprime en J·m^-2. Pour un système en rotation, il faudrait encore rajouter un terme  ω·dL. Ici, ω est la vitesse angulaire de rotation en rad·s^-1 et L le moment cinétique qui s’exprime en J.s·rad^-1). De plus, comme on l’a déjà dit on pourrait ajouter un terme m·g·h pour tenir compte de l’altitude h du solide

Un cas très particulier

Soit un corps pur (µ₁ = 0), d’extension infinie (γ = 0, φ = 0) et placé au ras du sol (h = 0). Supposons aussi qu’il soit immobile (ω = 0) et éloigné de tout champ électrique E_i = (0,0,0) ou magnétique B_i = (0,0,0). S’il est de surcroît liquide ou gazeux (σ_ij = -P·δ_ij et dV = V(dη₁₁ + dη₂₂ + dη₃₃), on retrouve alors l’expression la plus simple du premier principe :

dU = dQ – P·dV

Ceci illustre bien tout ce que recouvre le terme d’énergie interne. On comprend aussi très bien la portée très générale des raisonnements thermodynamiques. Car, ces derniers transcendent toutes les disciplines scientifiques : mécanique, électromagnétisme, chimie, biologie, etc.