Spin demi-entier

Le physicien autrichien Wolfgang Pauli (1900-1958) est à l’origine d’un principe, sans lequel les atomes n’existeraient pas. Son point de départ est la remise en cause de l’interprétation du nombre de raies spectrales émises par un atome. Cette théorie, basée sur la théorie de relativité, était l’œuvre du physicien allemand Arnold Sommerfeld (1868-1951). Pauli eut donc l’idée d’établir un principe d’exclusion. Un tel principe permettait de comprendre la structure en couches du tableau périodique des éléments de Mendeleev.

Tout démarre avec l’expérience de Stern et Gerlach qui utilise des noyaux d’argent de moment magnétique orbital nul. Cette expérience démontre l’existence de moments cinétiques demi-entier, J = ℏ/2. Ceci, en dépit du fait que la physique classique ne prévoyait que des valeurs entières. Pour expliquer ces valeurs demi-entières Sommerfeld et Alfred Landé avaient imaginé un modèle astucieux. Ils émirent ainsi l’hypothèse du cœur magnétique, qui concerne les couches électroniques internes entourent tout noyau atomique.

Rejet du modèle de Sommerfeld

Le noyau possède donc un moment angulaire interne R, différent du moment angulaire externe orbital K, provenant des électrons de valence. Le couplage vectoriel de ces deux moments angulaires produisait alors un moment angulaire total J = K + R. C’est ici qu’intervient Pauli à l’automne 1924. En effet, ce dernier pressent l’existence d’un lien profond entre deux problèmes. Premièrement, celui des structures en multiplets des raies d’émission de lumière par les atomes. Deuxièmement, celui de la construction du système périodique des éléments.

Pauli fait des calculs relativistes soigneux des rapports gyromagnétiques et des facteurs g correspondants. Il s’aperçoit alors que l’hypothèse du cœur magnétique conduit à des résultats en désaccord avec les valeurs expérimentales observées. Il va donc rejeter ce modèle. Et, revenir à l’idée que seuls les électrons de valence étaient responsables des effets magnétiques. Ceci va l’amener à introduire pour les électrons optiques une nouvelle observable n’ayant aucun équivalent en physique classique. Cette observable ne pouvait prendre que deux valeurs discrètes afin de rendre compte de l’expérience de Stern et Gerlach.

Un troisième nombre quantique

Pauli va aussi s’inspirer des idées du physicien britannique Edmund Clifton Stoner (1899-1967). Ce dernier publie le premier octobre 1924 un papier portant sur la distribution des électrons parmi les niveaux atomiques. Dans ce papier Stoner rejette le modèle de construction de la classification périodique des éléments publié par Niels Bohr en 1923. Car, un tel modèle se trouve en contradiction avec des expériences de 1924 faites par de Broglie et Dauvillier.

Stoner proposa ainsi d’ajouter aux nombres quantiques principal n > 0 et azimutal L (0 ≤ L < n), un troisième nombre quantique interne j. Ce nombre devait être tel que le nombre d’électrons associé à chaque sous-niveau de j donné soit égal à 2j+1. Toutefois, ces niveaux additionnels ne se manifestent, de manière équiprobable, qu’en présence d’un champ magnétique extérieur.

Puis, un quatrième

Dans la droite ligne de Stoner, Pauli rajoute un quatrième nombre quantique m_j. Il représente la composante du moment angulaire j dans la direction du champ magnétique. Grâce à ce nombre quantique additionnel, la structure en couches successives des atomes trouve une explication simple. En effet, chaque état possible se trouve identifié par ses 4 nombres quantiques |n, L, j, m_j>, avec -j ≤ m_j ≤ +j. L’idée est qu’un état ne peut être occupé que par un seul électron à la fois. Car, Pauli est toujours soucieux de trouver une explication au problème fondamental de Bohr.

Ce problème consiste à savoir pourquoi tous les électrons ne viennent pas occuper le niveau de plus basse énergie. Pauli va comprendre qu’il s’agit là, en fait une règle de prohibition. Car, la structure en couches de l’atome et les périodes du système périodique existent à coup sûr. D’où l’idée d’exclure la possibilité que plus d’un électron occupe un état |n, l, j, m_j> donné. Pauli introduit ainsi son fameux principe d’exclusion.

Principe d’exclusion

Un tel principe stipule, qu’en présence d’un champ magnétique fort, deux électrons ne peuvent partager le même jeu de nombres quantiques |n, l, j, m_j>. La présence d’un champ magnétique fort était nécessaire dans l’argument de Pauli. Car, dans ce cas on pouvait considérer que les électrons étaient bien dans des états individuels stationnaires. Autrement dit, ils ne pouvaient pas interagir entre eux. Or, les 4 nombres quantiques |n, L, j, m_j> ne peuvent être définis en toute rigueur que pour un faible champ magnétique.

En présence d’un champ magnétique fort, il faut remplacer le nombre quantique j par un nombre quantique magnétique m_L. Celui-ci représente la composante du moment magnétique orbital dans la direction du champ appliqué. Le nombre quantique m_j doit être remplacé par un autre nombre quantique m_S. Ce dernier ne pouvait toutefois prendre que deux valeurs égales à ±1/2. Avec ces nouveaux nombres quantiques, le moment angulaire total devenait j = L + S avec S = ±1/2. Il se trouve donc que les nombres quantiques sont différents selon la valeur du champ magnétique appliqué.

Quatre nombres quantiques par état

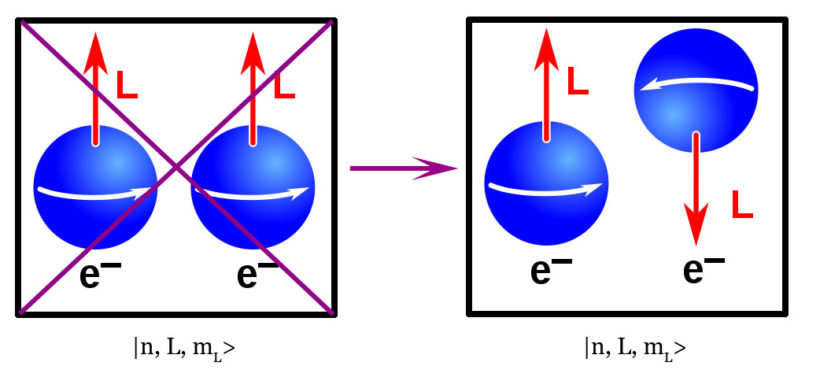
Il n’en reste pas moins qu’il faut en avoir toujours 4 et non 3 comme auparavant. Par conséquent, quelle que soit l’interprétation de ces 4 nombres quantiques, ils existent pour toute valeur du champ magnétique appliqué. Pauli va aussi réaliser que son principe d’exclusion d’un seul électron par état fonctionne de manière universelle. Que cet état soit indexé par les nombres |n, L, j, m_j> ou par les nombres |n, L, m_L, m_S>. Le principe d’exclusion permet aussi d’expliquer l’absence d’état triplet (j = 1) dans le spectre optique de l’atome d’hélium. Le schéma suivant explique pourquoi :

Ainsi, pour n = 1, les seules valeurs possibles sont L = m_L = 0. Pour avoir j = 1 (état triplet) il faudrait que les deux électrons aient s = +1/2. Cela signifie qu’ils auraient alors le même jeu de nombres quantiques |1, 0, 0, 1/2>. Le principe d’exclusion de Pauli interdit donc un tel état final. Ceci est parfaitement confirmé par l’expérience. Car, l’hélium n’existe bien que sous forme de singulet (j = 0). Or, c’est bien la seule configuration autorisée par le principe d’exclusion. De fait, les deux électrons ont dans ce cas des nombres quantiques différents.

Construction du tableau périodique

Conventionnellement, on représente la valeur s = +½ par une flèche pointant vers le haut. De même, une flèche pointant vers le bas représente la valeur s = -½. On a donc |↑> = |1, 0, 0, +½> et |↓> = |1, 0, 0, ½2>. On remarquera qu’il est impossible de rajouter un troisième électron dans la case d’énergie la plus basse notée 1s = |1, 0, 0>. Ceci parce que le quatrième nombre quantique ne peut prendre que deux valeurs s = ±1/2. Quoique l’on fasse, on aura donc forcément deux jeux de nombres quantiques identiques. Le principe d’exclusion de Pauli interdit cela.

Le troisième électron (lithium) devra alors aller dans l’état 2s = |2,0,0> de plus haute énergie. L’état 2s ayant L = m_L = 0, ne pourra comme l’état 1s ne peut accueillir que 2 électrons (béryllium). Le cinquième électron (bore) devra donc aller dans l’état 2p. Lui, possède par contre trois sous-états : |2,1,1>, |2,1,0> et |2,1,+1>. Il peut donc accueillir 3×2 = 6 électrons avant d’être plein (néon). L’état (2s,2p) est donc rempli avec 2+6 = 8 électrons. Le onzième électron (sodium) devra se trouver dans l’état 3s = |3,0,0> et ainsi de suite.

Généralisation à champ magnétique nul

Le principe d’exclusion de Pauli forme donc la clé de voûte du tableau périodique des éléments. Or, ce dernier existe même en l’absence de champ magnétique. Pauli invoque donc le principe d’invariance des poids statistiques des états quantiques. Cela lui permet d’étendre ces résultats aux champs magnétiques faibles, voire nuls. Il imagina ainsi une transformation adiabatique au cours de laquelle l’intensité du champ magnétique se trouve progressivement réduite. De la sorte, la caractérisation des états quantiques individuels par quatre nombres quantiques reste préservée à tout moment.

Toutefois, Pauli commet ici une faute méthodologique. Car, il se trouve que le principe d’invariance adiabatique ne s’applique qu’aux systèmes périodiques ou multipériodiques. Malheureusement, un atome à N électrons constitue un système apériodique. Toutefois, la série de nombres entiers en 2×n² = 2, 8, 18, 32… pour n = 1, 2, 3, 4 est bien observée expérimentalement. Par conséquent, son principe d’exclusion contribue à lever le voile sur l’origine de la périodicité des éléments. Cette description de la structure atomique au moyen de 4 nombres quantiques par électron va donc être adoptée de manière unanime.

Découverte d’une nouvelle observable physique

On remarquera que Pauli n’associait pas le nouveau moment angulaire s = ±1/2 au cœur de l’atome comme le faisait Sommerfeld et Landé. C’était bien une propriété des électrons de valence. Cela suggérait donc l’existence d’une nouvelle observable purement quantique. Ne pouvant prendre que deux valeurs possibles, une telle observable n’avait aucun équivalent classique. Ceci permettait de rendre compte de l’expérience de Stern et Gerlach avec des atomes d’argent de moment orbital nul. Cela ouvrait aussi une voie royale pour découvrir l’existence du spin de l’électron.

Référence

Max Jammer, “The conceptual development of quantum mechanics”, McGraw-Hill, New-York (1966).